分类讨论思想在高一函数教学中的应用

分类讨论思想在高一函数教学中的应用

王忠廷

德州市陵城区第一中学，德州 陵城 253500

摘要：分类讨论思想是重要的数学学习思想，在高中的数学教育中占据着重要地位。其思想主要体现在从各个角度全面地讨论同一问题，力求得出某一问题的全部可行解，主要适用于题目较为复杂，涉及可行解众多的问题。而在函数问题中，分类讨论思想则更是常用，由于高一数学涉及的函数已经较为全面和复杂，若想将问题如函数单调性、极值、变化趋势等讨论清晰正确，则要求学生必须熟练掌握分类讨论思想。

关键字：分类讨论思想；高一函数教学；应用

引言：

分类讨论是处理复杂问题的基本思想之一，通过对于问题仔细地分析，将题目中所提供地要素抽象为数学符号，并根据题目特征将其分类进而逐一对其讨论。而针对函数教学来说，则需要根据其参数的不同取值对函数整体的影响，将其按照自身所提供的性质特征进行讨论，将每一步的计算与化简都分析清楚，才能够保证所做题目的正确性。教师也应该注重培养学生的分类讨论能力，配合数形结合的能力，将为学生打好数学基础，学好高中函数知识提供有力的支持。

一、分类讨论思想的意义

分类讨论思想与数形结合思想相同，都是打好高中数学基础、学好高中函数的重要思想。数形结合的思想是将图像与函数解析式结合，辅助学生求解函数问题；而分类讨论思想更像是对于问题的全局性把控，像是军师般派兵布阵的全面考虑问题，把函数问题中每种有解的可能性全部加以讨论，是全面的严谨的数学思维，是将函数问题彻底讨论清晰的数学基础。

（一）分类讨论原则

在对于问题进行分类讨论的时候，需要注意几个方面的问题，即注意分类讨论的基本原则：不重复不遗漏、同一分类标准、由简至深讨论，以下对于上述三点进行详细讨论^[1]。

1.不重复不遗漏

在使用分类讨论思想解决数学问题时，要注意对被讨论对象的分类需要做到，不重复也不遗漏的分类。例如在对于整数的分类时，整数可以分为三类：正数、零、负数，不能将零遗忘也不能擅自添加分类。再比如需要对所有平行四边形进行分类讨论，就不能将其分为矩形和菱形，因为有些平面图形如正方形就同时满足两个分类，类似于这样的分类标准就是不严谨的、不科学的。

2.同一分类标准

在对某一问题进行分类讨论的过程中，除了严谨的分类个数，还需要科学统一的选取分类标准，在对于同一问题的讨论中，不建议采取不相同的分类标准，这样只会给求解问题带来困难，在某种程度上也使得分类讨论的做法失去了实际意义。例如求解一个关于三角形分类的问题，需要根据问题的问法来确定分类标准是按照角度大小分类，还是按照边长的长度分类。将其分为锐角、直角、钝角，还是将其分为普通、等腰、等边三角形，都需要严谨的思考和分类，切记将不同的分类标准应用于同一问题中，这样会打破分类规则使分类失效。

3.由简至深讨论

对于相对复杂的问题而言，一般由于问题复杂参数较多无法直接入手，则可以采用由简至深的分类方式对问题进行解析。现对问题中较为简单的部分进行作答，再在已有答案的基础上对复杂问题进行化简，以达到分类讨论的效果。

（二）分类讨论类型

在讨论了分类的基本方式之后，对于高一函数的学习而言，分类的类型一般为：由于函数一般概念引起的分类，由性质或定理引起的分类，由数学运算规则引起的分类，由其对应图像不确定引起的分类，以及由函数内部参数变化而引起的分类。

（三）分类讨论步骤

应用分类讨论思想求解函数问题时，一般可分为以下步骤：首先根据题目所给信息和条件，确定出需要分类讨论的对象以及参数范围；其次根据上述分类原则和方式对其进行分类；再次根据由简至深的讨论原则层层分析；最后对于计算结果逐层总结归纳得出最终答案^[2]。

二、求解函数问题的示例

在高一的数学学习中有着众多复杂的函数，其中指数与对数函数是难度相对较大的，其复杂的性质以及运算规则，让很多学生无法牢固掌握，从而在高中刚开始的阶段就对数学产生了畏惧心理，现针对对数函数而言，列举若干个相关分类讨论思想应用的实例，以帮助学生理解分类讨论思想求解函数问题。

（一）对底数进行讨论

根据高一数学教材中的相关对数函数知识点，进行分类讨论思想的实例演示：例如比较对数 以及 的大小其中(a>0，且a )。对其进行分析有：想要判断对数函数的大小需要根据其单调性，因此对底数a进行讨论，当a>1时，对数函数单调递增；当0<a<1时，对数函数单调递减。因此该问题的解为：当a>1时， < ；当0<a<1时， > 。

（二）对参数进行讨论

设函数f(x)= ，若有0<m<n，且f(m)>f(n)，证明mn<1^[2]。对题目进行分析有：根据函数f(x)对于函数图像及其性质可知f(x)的单调性，由于当x>1时，f(x

)单调递增；当0<x<1时单调递减。故对其分类讨论得，由于0<m<n，且f(m)>f(n)，故m>1，n>1不可能。当0<m<n<1时，显然mn<1成立。当0<m<1，n>1时，由f(m)>f(n)得 > 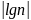，所以lgm ，即m< ，从而mn<1，综上所述mn<1。

三、结束语

函数学习是高中数学学习的重难点，教师需要帮助学生进行知识点的总结与归纳，必要时还可以针对不同数学思想或解题方式开展专题讲解，对学生进行重点和难点的解析。让学生在高一阶段就打下良好的数学基础，养成良好的数学学习思维和习惯，这样可以在今后的高中乃至大学的学习数学学习中，达到事半功倍的效果。

参考文献：

[1]巨海波.分类讨论思想在高中数学教学中的应用分析[J].华夏教师,2018(23):34-35.

[2]刘祝芸.关于分类讨论思想在高中数学解题中的应用思考[J].经贸实践,2016(19):80.