浅析数学分析中分段函数分界点的连续性与可导性

浅析数学分析中分段函数分界点的连续性与可导性

杨橙

第八中学 广东省，湛江市

摘要：本文运用实例探究了数学分析中分段函数分界点的连续性与可导性，从而丰富了数学分析中有关分段函数分界点的连续性与可导性的内容.

关键字：分段函数; 分界点 ; 连续性 ; 可导性

1 引言

1.1 本文背景

由于分段函数的特殊性,它的研究不仅牵扯的知识面广、方法多变, 且综合性强，利用以前学过的函数的连续性和可导性的知识来进一步探讨分段函数分界点的连续性和可导性,相关内容参见文献[1-9].

1.2 本文主要内容及意义

本文从7个方面探讨了分段函数分界点的连续性和可导性.

2 分段函数分界点的连续性问题

2.1 用函数连续性定义判别分段函数分界点的连续性

定义1^[1] 设函数 在某 有定义，若 ，则称函数 在点 处连续.

文献[1]给出函数 在点 处连续的三个条件：

a. 函数 在点 处要有定义；

b．极限 存在；

c. .

例1讨论函数

在 处的连续性.

分析 此分段函数在分段点 左右两边的函数表达式相同，因此其在 左右两边的极限相等，所以其在 的极限一定存在，然后再根据文献[1]给出的三个条件判断其 的连续性.

解 (1)函数的定义域为 ，故函数在 有定义;

(2) ;

(3) ，即 .

因此 在 处同时满足定义中的三条，所以 在 处连续.

2.2 用函数单侧连续性判别分段函数分界点的连续性

定义2^[1] 设函数 在某 内有定义，若 ，称函数

点 处左连续.

定义3^[1] 设函数 在某 内有定义，若 ，称函数 在点 处右连续.

定理1^[1] 在点 处的连续的充要条件是 在点 处既要左连续又要右连续.即

例 2 设函数

试分别讨论 在点 与 处的连续性.

分析 此分段函数在分界点 和 左右两边的函数表达式都不同，因此不能用定义1去求,此题可以用定理1求，只有证明分段函数分界点的左右连续且相等就可以证明此分段函数在分界点连续.

解 在 处：由已知当 时， 为初等函数.又 为函数定义区间上的点,则 .所以 在 处为左连续

又因为 ，所以 在 处也右连续.

由于 在 处既左连续又有连续，故 在 处连续.

在 处：同理可知，在 处， 为初等函数，又 为函数定义区间上的点，且 .所以 左连续,因 ，所以 在 处不右连续,

由于 在 左连续但不右连续，故 在 不连续.

3 分段函数分界点的可导性问题

3.1 用导数定义判别分段函数分界点的可导性

定义4^[1] 设函数 在点 的某邻域内有定义，若极限 存在，则称函数 在点 处可导，并称该极限为函数 在点 处可导，记作 .

例3 设函数

判断 在 的可导性.

分析 分界点两侧的函数表达式相同，因此用可导的定义去求.

解

在 处连续

， 在 处可导.

3.2 用函数单侧可导性判别分段函数分界点的可导性

定义5^[1]设函数 在点 的右邻域 上有定义，若右极限 存在，则称函数 在 处右可导，该极限值为 在点 的右导数，记作 .

定义6^[1]设函数 在点 的左邻域 上有定义，若左极限 存在，则称函数 在 处左可导，该极限值为 在点 的右导数，记作 .

定理2^[1] 若函数 在点 的某邻域内有定义，则 存在的充要条件是 与 都存在，且 .

例4 设函数

求 在 处的可导性.

分析 此分段函数在分界点左右两侧的函数表达式不同，因此不能用导数的定义求，只能用左右导数相等的性质求.

解 ， ，即 ，

在点 处连续.

， ，

， 在点 处可导

例5 设函数 ,判别 在 与 处的可导性

分析 函数 看似不是分段函数，但去掉绝对值后函数其 实是一个分段函数，要求分段函数在分界点的可导性首先要求其在分界点是否连续，若不连续则必不可导，若连续，再按可导的定义求导、判断.此分段函数在分段点的两侧的函数表达式不同，所以要用定义分别求出分段点的左右导数，再判断.

解 即

, 即左连续也右连续，

在 处连续，同理可证 在 处连续，

根据可导的定义求得

， ，

， 在 处可导

同理可得 ， ，

在 处不可导

注 这说明若分段函数在其分界点连续，并不一定在分界点可导.但如果分段函数在分段点可导则必连续.即连续是可导的必要条件，而非充要条件.

3.3 用可导与连续的关系判断分段函数分界点的可导性

例6 设函数

判断 在 处的可导性.

分析 分段函数分界点连续是可导的必要条件，要证明可导则首先要证明其在分界点上连续.

解 ，

因为 在 处不连续，所以一定不可导.

但有些学生可能会犯这样的错

当 时，

从而 在 处可导，且

分析 上述解法错在事先没有判断 在 的连续性.

定理2 ^[5] 若函数在点 的某邻域有定义，且 都存在，则 在 处一定连续.

例7 设分段函数

判断 在 处的可导性.

分析 要判断分段函数分界点的可导性，首先要判断其在分界点的连续性，因为此函数在分界点两侧的函数表达式不同，所以再用单侧可导性来判别函数的可导性.

解

在 上连续，

， 在 处不可导.

注 在定理中，仅要求左、右导数存在，并不要求一定相等，如例7中 在分界点 的左右导数存在，即使 ，也可以证明其连续.

3.4 用分段函数分界点的可导性确定待定参数

例8 设函数

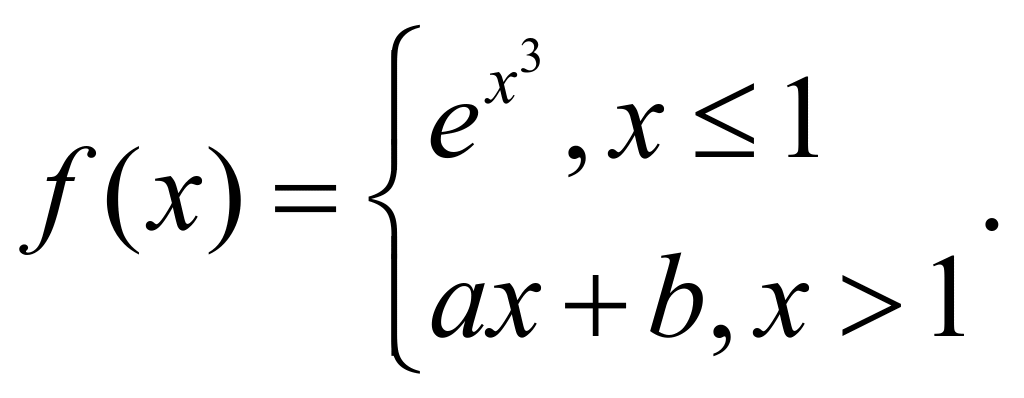
若要 为可导函数，应如何选择 ， ？

分析 若 在定义域 为可导函数，说明 在每点都可导，即 在 处也可导，由 可导性与连续性关系得 在 处也连续，则可由 在 可导，且连续两个条件求出 , .

解 若 为可导函数，则在 定义域内处处可导，即其在 处也可导，由可导与连续的关系，知 在 连续.则有

故有 即 ，又 在 可导，则

因此当 , 时， 存在，从而 为可导函数.

注 上例很好的运用了可导一定连续的这一性质，但是其实只要左右导数都存在，就可以推出连续的性质.

4 小结

本文主要阐述了如何判断分段函数在分界点的连续性和可导性.如可以用函数连续性的定义和函数单侧连续性来判别其分段函数的连续性.而要判断分段函数分界点的可导性则有多种方法，如可用函数导数定义、函数单侧可导性、函数可导与连续的关系和导数极限定理来判别分段函数分界点的可导性，并且一般用导数极限定理比用导数定义判别更加简单.

参考文献

[1] 高尚华.数学分析上册(第三版)[M].北京:高等教育出版社,1987:12-91.

[2] 高尚华.数学分析下册(第三版)[M].北京:高等教育出版社,1987:12-110.

[3] 林远华.分段函数的连续性与可微性[J].河池师范高等专科学校学报,2000, 20(2):26-29.

[4] 王琦.分段函数分界点处的可导性问题[J].齐齐哈尔师范学院学报. 1996,16(4):18-20.

[5] 辛兴云.判断“分段点”可导性的一个简便方法[N].河北广播电视大学学报,2000,5(2):55-57.

[6] 胡晶.王可宪.1994.分段函数在分段点可导的一个充要条件[J].承德民族师专学报,1994,10(2):26-27.

[7] 李艳娟.高等代数中分段函数问题研究[J].辽宁教育学院学报, 1997,14(5):59-62.

[8] 张红卫.浅析分段函数[J].山西广播电视大学学报,2000,1(3):60-61.

[9] Patrick M.Fitzpatrick．Advanced Calculus：A course in Mathematical Analysis[M]．Beijing：China MachinePress，2003:113－140．

9