德阳市华山路学校 618000
引言:
小学数学学习中,其抽象性和小学生的形象思维较弱形成一对矛盾体,随着小学生学习阶段的不断深入,特别是进入到应用题阶段,受到识字数量的影响,无法准确的理解题目的意思,对于解决问题造成较大的麻烦。如何让小学生能够理解数学题意,更好更快的认识数学,解决问题呢?本文重点讲解画示意图在小学数学教学中的应用,希望能够在小学数学教学中引起共鸣。
关键词:小学数学 示意图
画示意图在小学数学教学中的应用十分广泛,心理学研究表明,小学生的思维是以具体形象思维为主,具体的、直观的现象更能让学生接受、理解和掌握。通过画图来架起学生形象思维和抽象思维之间的桥梁。
我们在具体问题的题意理解、数量关系分析、问题的解决策略,都离不开画示意图这一几何直观手段。运用图示表征题意和分析数量关系,反应了数形结合的数学思想和用画图解决问题的重要策略。利用画示意图可以把抽象的文字形象化,把隐藏的的数量关系显现化,把复杂的图形简易化,能很好的帮助我们找到解决问题的有效途径。
那么,什么是示意图呢?我们通常用“圆圈"方框""线段"等这样的图形代替题目中的事物数量,清晰地描述事物发展的过程,揭示事物数量之间的关系,为解答问题提供了直观说明和重要依据。示意图的特点就是简单明了,重点突出,而且直观形象。
如何很好的引导学生运用画示意图的策略解决问题,清晰的表示出数量关系及解决问题的思考过程与结果呢?
其实,在我们一年级们的时候孩子已经在接触示意图了,见下图1,小丑拿气球数量的问题:小丑左边拿了3个气球,右边拿了1个气球,合起来一共有4个气球。在气球图的下面又以圆片代替气球,先摆3个圆片,再摆1个圆片来表示气球的数量,合起来就是4个圆片。
为何要用圆片代替气球?那是因为气球只能解决气球这一个问题,而圆片是可以代替苹果、汤圆、小鸡等等很多事物,让孩子直观的得出结果。这里的圆片,其实还可以替换成三角形、正方形、星星等都可以。在小学阶段,我们解决问题的时候,需要直观形象的支撑,所以当我们没有实物的时候,我们就可以画出代表实物的简单示意图帮助我们解决问题。这种实物替代图在数量上与实物一一对应,以离散量的形态呈现。

图1 小丑的气球
又如比较套圈多少的例题:小华套中了12个圈,小雪套中了7个圈,要求计算小华比小学多套中几个?教材呈现了小雪7个圆,小华12个圆的示意图,让孩子一眼就能看出多了5个,并且正确的列出算式。

图2 比较圆圈多少
再比如比较两个班级小红旗数量多少的问题: “一班得了12面小红旗,二班比一班多得3面。二班得了多少面?”人教版教材根据题意呈现了下面得示意图。

图3 比较红旗多少
像上面这样的题目给出具体的数量我们可以一一对应得画出相应的图形,他们的关系也就一目了然,可以帮助孩子快速的找到方法解决问题,并且可以通过画示意图来验证答案。
随着孩子年级的升高,画的示意图也就越来越复杂,不再仅仅局限于点对点(离散量)的关系,这个时候开始出现线段图(连续量),相比较而言,离散量的实物替代图孩子们更为熟悉,掌握起来简单易行,操作方便,而作为连续量的线段比较抽象,需要专门的学习过程来积累经验。
例如下面的例题: “妈妈的钱买6元一个的碗,正好可以买6个。用这些钱买9元一个的碗,可以买几个?”,孩子们在刚开始自己画得时候就不注意理解题意,“这些钱”是多少钱?前后两次的钱一样吗?那我们在画图的时候就要注意两条线段一定是一样长。第一条线段里面的每一份代表每一个碗6元,而第二条线段每一个碗9元,那么9元就应该比6元长一些,对于中低年级的孩子来说,在画这种线段图的时候大概意思描述到位、关键的关系能够看得出来即可,不要求完全准确。参考图4所示,通过同样长的线段(表示总量)表示两次买碗的钱数是相等的,再以“每个碗6元”的线段和“每个碗9元”的线段长短不同来做一个对比,这样才能帮助孩子建立直观形象的思考过程,正确的列出算式,解决问题。

图4 线段计算
随着小学阶段数学学习的不断深入, 在探讨“分数的基本性质”时,我问孩子们 、
、 、
、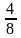 ,哪一个分数最大?哪一个最小?为什么?大部分孩子凭借着以前整数的比较大小的经验,脱口而出:
,哪一个分数最大?哪一个最小?为什么?大部分孩子凭借着以前整数的比较大小的经验,脱口而出: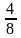 最大,
最大, 最小。我没有立马给予评价,而是让孩子们通过折一折、画一画、比一比,再判断。可以画同样长的线段,同样大小的长方形、圆都可以(如下图5)。孩子们很快就得出结论,惊呼到居然一样大。这极大地激发了孩子的学习兴趣,让他们感受到数学原来是如此的神奇,居然隐藏了这么多可爱的秘密。
最小。我没有立马给予评价,而是让孩子们通过折一折、画一画、比一比,再判断。可以画同样长的线段,同样大小的长方形、圆都可以(如下图5)。孩子们很快就得出结论,惊呼到居然一样大。这极大地激发了孩子的学习兴趣,让他们感受到数学原来是如此的神奇,居然隐藏了这么多可爱的秘密。

图5 分数比例示意图
画示意图的功能远远不止于此,不仅可以快速的解决像上面这些题型,根据现有的信息可以直接找到答案,还可以应用于从正面直接计算比较棘手的难题,并且让难题变得很容易理解,只要肯开动脑筋,孩子们敏锐的眼光定能发现其中的规律。比如这样的一道计算题:
 +
+ +
+ +
+ +
+ +……
+……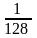 =( )
=( )
如果用通分的方法来做,这个就太麻烦了,所以这个时候画图就可以来帮帮我们。如下图6,我们发现它把这整个图形作为单位“1”,图上空白的是 ,那么剩余的部分就是1-
,那么剩余的部分就是1- =
=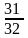 ,即是
,即是 +
+ +
+ +
+ +
+ =1-
=1- =
=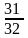 .通过这类简单一点的算式可以推出
.通过这类简单一点的算式可以推出 +
+ +
+ +
+ +
+ +……
+……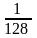 = 1-
= 1- 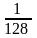 =
= 。
。 
图6 分数计算示意图
这种图我们可以取名为面积图,就是先根据数据画出整体图形,再进行分割,最后标注所求问题(也可省略)。面积图一般用于体现整体与部分之间。
例如和面积计算有关的数学题:“长方形花圃原来长6米,修建时增加了2米,面积增加了8平方米,原来的花圃面积是多少平方米?”显然,直接计算,无法计算出原有的花圃的面积,但是如果采用合适的示意图,则会有很明显的效果,见下图7。

图7 花圃有多大
从上图可以看出,新增长方形面积为8平方米,花圃的宽度为8÷2=4米,那么原有花圃的面积就很容易计算为6米×4米=24平方米。对于类似的面积求解的数学题,均可以采用示意图的方法进行解决。
然而,孩子们想要正确的画出示意图非一日之功,是需要系统学习的。从一年级开始,我就让孩子们能摆实物的一定要摆,能画图的一定要画,孩子们在纸上自己通过涂一涂、画一画,可以帮助他们理解题意,也调动了他们参与学习的积极性,学生只要能正确的用图表示出自己是如何思考的,能让其他同学看懂图意,对于图的样式不作统一要求。
后记:
教学中不仅仅要立足于今天,更要着眼于明天,教师要非常重视学生的画图指导与训练,只有把图示学习作为一个长期的规范的工程来操作,让孩子们养成良好的学习习惯,孩子们的画图策略才能渐渐形成,几何直观才有可能落体生根,才能让孩子们更加快速的遨游在数学知识的海洋。
主要参考文献:
[1] 徐军 示意图在小学数学教育中的有效应用研究[J],《名师在线》,2019(000)016:18-19
[2] 李丹. 例谈示意图在小学数学教学中的价值与运用[J]. 课程教育研究, 2014, 000(035):173-173.
[3] 义务教育教科书 数学 一年级下册,部编人民教育出版社2012年10月第1版
[4] 义务教育教科书 数学 三年级上册,部编人民教育出版社2014年6月第1版