中国电子科技集团公司第二十研究所 陕西西安 710000
摘要:本文提出了一种由无人机传感系统所得到的测量数据转变为控制系统所需的导航数据的矩阵计算方法,之后提出了无人机经向和和横向运动的数学模型,最后基于![]() 聚合理论,设计了一种鲁棒控制器,并通过模拟仿真得到了控制效果,仿真结果表明该控制器具有一定的鲁棒性,可以在各类无人机等运动平台中得到广泛应用。
聚合理论,设计了一种鲁棒控制器,并通过模拟仿真得到了控制效果,仿真结果表明该控制器具有一定的鲁棒性,可以在各类无人机等运动平台中得到广泛应用。
引言
如今无人机平台在越来越多的领域取得广泛应用,各项相关技术也随之迅猛发展,飞行控制系统设计便是其中一个重要研究方向。由于无人机飞行环境的不确定性以及内部传感器的不稳定性等因素,飞行控制系统必须能够在各类外部干扰的条件下保持稳定,即保持系统鲁棒性。
无人机内部通过装载各类传感设备,为其控制系统提供所需参数,如速度、高度、倾角等。为提升测量数据的可靠性和准确性,传感器的配置通常具有测量数据非正交且数据冗余等特点。因此无人机的控制系统要在传感系统提供的大量冗余数据中进行过滤,而具体选择哪些数据则要根据无人机的特点和需求综合考虑。通常情况下,无人机控制系统和传感系统的功能示意图如图1所示。

由此,无人机的控制系统设计主要可分为两个部分,其一是在传感系统得到的众多冗余数据中选择适当的参数并开发数据聚合算法,其二是设计具有一定鲁棒性的控制系统。
参数选择
一种比较成熟的方法是将描述无人机运动的向量集合视为一种类似圆锥体的形式[1],各单轴传感器的测量向量均沿圆锥形的母线排布。综合考虑系统精度与成本,可以使用6个传感器[2],其中5个传感器沿圆锥形法线方向排布,1个传感器沿圆锥形轴线方向排布,测量数据组成的坐标系如图2所示,其中![]() 表示导航坐标系;
表示导航坐标系;![]() 表示测量坐标系(
表示测量坐标系(![]() 沿法线方向,
沿法线方向,![]() 沿轴线方向向下。
沿轴线方向向下。

无人机内部传感器测量数据和所需的导航信息的关系可由下式表示:
![]() (1)
(1)
其中,![]() 为角速度在测量坐标系中的投影向量,
为角速度在测量坐标系中的投影向量,![]() 为角速度在导航坐标系中的投影向量;
为角速度在导航坐标系中的投影向量;![]() 为传感器数量;矩阵
为传感器数量;矩阵![]() 表示了导航坐标系向测量坐标系的传递矩阵,见式(2)。
表示了导航坐标系向测量坐标系的传递矩阵,见式(2)。
 (2)
(2)
由式(1)可知,投影向量![]() 可表示为:
可表示为:
![]() (3)
(3)
基于广义逆矩阵算法可知:
![]() (4)
(4)
无人机的数学模型
一种无人机的线性数学模型可由下式表示:
![]() (5)
(5)
无人机的纵向动作表示为向量![]() :
:
![]()
其中,![]() 为水平和垂直方向的真实速度;
为水平和垂直方向的真实速度;![]() 为倾斜角速度;
为倾斜角速度;![]() 为倾斜角度;
为倾斜角度;![]() 为飞行高度;
为飞行高度;![]() 为电机运行角速度。
为电机运行角速度。
无人机纵向动作由升降舵以及引擎的工作状态共同影响,控制向量可表示为:
![]()
其中,![]() 表示升降舵的偏差因数,
表示升降舵的偏差因数,![]() 表示引擎的输出功率因数。输出向量可表示为:
表示引擎的输出功率因数。输出向量可表示为:
![]()
其中,![]() 表示真实速度。
表示真实速度。
其纵向动作可由如下公式表示:
 (6)
(6)
由此可知,矩阵A及矩阵B可表示为以下公式:
 (7)
(7)
 (8)
(8)
可基于无人机的数学模型,即根据式(5)设计鲁棒控制系统,矩阵![]() 、
、![]() 中的参数值可由MatLab中的飞行仿真程序得到[3]。
中的参数值可由MatLab中的飞行仿真程序得到[3]。
对于无人机模型的横向运动,状态向量可表示为:
![]()
其中,![]() 和
和![]() 分别表示侧滚和偏航的角速度,
分别表示侧滚和偏航的角速度,![]() 和
和![]() 分别表示侧滚和偏航的角度,控制向量表示为:
分别表示侧滚和偏航的角度,控制向量表示为:
![]()
其中,![]() 和
和![]() 分别表示侧翼和方向舵的偏移角度。输出向量可表示为:
分别表示侧翼和方向舵的偏移角度。输出向量可表示为:
![]()
其横向动作的公式如下:
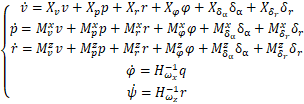 (9)
(9)
根据式(9)可知,此时矩阵A及矩阵B表示为:
 (10)
(10)
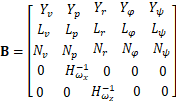 (11)
(11)
控制系统设计与仿真
用于实现无人机控制的聚合算法由无人机的数学模型和鲁棒控制系统模型共同组成,二者的传递函数分别用![]() 和
和![]() 表示。该系统通常具有2个输入和2个输出变量,外部输入变量
表示。该系统通常具有2个输入和2个输出变量,外部输入变量![]() 由诸如指令信号、扰动和噪声等组成;输入变量
由诸如指令信号、扰动和噪声等组成;输入变量![]() 表示控制信号;输出变量
表示控制信号;输出变量![]() 用于表示控制结果的好坏,例如当
用于表示控制结果的好坏,例如当![]() 表示控制结果与输入指令的误差时,在理想条件应有
表示控制结果与输入指令的误差时,在理想条件应有![]() ;输出变量
;输出变量![]() 表示观测信号,用于系统反馈。用符号
表示观测信号,用于系统反馈。用符号![]() 表示由
表示由![]() 的传递函数,基于
的传递函数,基于![]() 控制理论进行控制系统设计的主要任务便是得到函数
控制理论进行控制系统设计的主要任务便是得到函数![]() ,使范数
,使范数![]() 最小,概括来讲,其优化准则如下式所示:
最小,概括来讲,其优化准则如下式所示:
 (12)
(12)
其中,![]() 、
、![]() 、
、![]() 为灵敏度函数的加权传递函数。矩阵中的三个行向量分别表示灵敏度函数,控制偏差的灵敏度函数,以及对应补偿的灵敏度函数。
为灵敏度函数的加权传递函数。矩阵中的三个行向量分别表示灵敏度函数,控制偏差的灵敏度函数,以及对应补偿的灵敏度函数。
使用上述优化准则,可以解决如无人机控制等实际应用场景中的复杂优化需求。
本文针对无人机在纵向运动中的速度和高度数据利用Matlab进行了模拟仿真,具备鲁棒控制器的聚合算法对于无人机速度和高度控制的仿真结果分别如图3和图4所示,图中虚线表示参数受到扰动的模拟系统,实线表示理想对照系统,模拟结果表明本文所述的控制系统能够在一定程度上消除在实际应用场景中参数的扰动对控制系统带来的不良影响。


结论
仿真结果表明,将具备冗余配置的传感器系统和鲁棒控制系统相结合,可以提高无人机导航系统的可靠性以及控制系统的鲁棒性,改善无人机在复杂真实环境下的运行状态,能够在众多领域开展实际应用。
参考文献
[1]A.D.Epifanov. Redundant Systems of Aircraft Control[J]. Moscow: Mashinostroenie,1978.p.178.
[2]O.A.Sushchenko. Nonorthogonal Redundant Configurations of Inertial Sensors [C]. IEEE 4th International Conference Actual Problems on Unmanned Aerial Vehicles Developments,October 17-19,2017,73–78.
[3]J.C.Jeromel. Convex Analysis of Output Feedback Control Problems: Robust Stability and Performance[C]. IEEE Transactions on Automatic Control,vol.41,no.7, 1996,903–1003.