学习能力综合评价模型的构建

学习能力综合评价模型的构建

卢思怡，杨滟滟，曾静怡，余丹，王国婧

中南大学计算机学院，湖南省 长沙市 410000

雷向东副教授

中文摘要：本文通过对历年来的学习能力构成因素和组成成分相关研究的文献进行整理，总结出了组成学习能力的四大系统，分别是动力系统，行为系统，调节系统，环境支持系统。研究通过指标体系的构建设计分发层次分析法专家问卷来确定各个指标的权数。问卷的数据处理后均通过一致性检验，成功构建大学生学习能力综合评价体系，为大学生智能学习规划平台的搭建提供了模型依据。

1.研究目的

进入大学，可供自由支配的时间变多，学习方式也发生了变革，学习不再是单纯的死记硬背和反复记忆，受到的影响因素也变多。学习能力既是基础能力，又是核心能力，是大学生未来发展的核心竞争力。所以对大学生学习能力的组成因素的研究和评估成为了一个重要的课题。

本文希望通过研究大学生学习能力的构成指标，通过层次分析法构建大学生学习能力评价体系，以此为搭建智能学习规划平台提供大学生学习能力评价模型支持。

2.文献综述

学习能力的影响因素和组成指标，诸多文献出于不同角度有不同的理解。本文综述了一些国内研究的文献的成果。

魏萍认为学习能力可类比物理学中“力”的特征要素进行分析，分为作用点、方向、大小、速度、持续时间及效果等六方面。

李清平认为信息时代的大学生学习能力是由大学生在学习过程中所必需的八种能力所组成。

3.模型的构建方法

近年来，在教学与学生质量评价模型方面主要包括加权平均法、单项因子评价法、多元线性回归、层次分析法、灰色关联法、模糊聚类分析法、神经网络结构等方法。本文选取了层次分析法、灰色关联法、模糊聚类分析法进行介绍，并做出比较。

3.1层次分析法

3.1.1层次分析法的含义

层次分析法（Analytic Hierachy Process，AHP）是国外Saaty于20世纪70年代末提出的一种新的系统分析方法，目的在于将复杂问题系统化，简化为几个简明扼要的层级。

3.1.2层次分析法的实施步骤

①确定要研究的问题和分层

首先要确定研究的主要问题，明确研究的问题定义，弄清楚决策的目的，充分掌握研究问题的方向，提出总目标，对评价要素分层。

②建立层次结构

以层次分析法处理决策问题，首先需要将决策问题的目标特性分写成上下串联的层级，且每层级中需尽可能纳入与总目标相关的所有决策属性，要考虑完整性，每个层级内要考虑所有决策元素的不同性质。

③进行重要性比较，构建判断矩阵

美国运筹学家萨蒂（T.L.Satty）在20世纪70年代首次提出9标度层次分析法。9标度层次分析法的基本方式就是对各层次因素重要性进行两两对比，即对每一层下的所有因素进行重要性等级比较，假设当前层次上的因素为 ，相关的上一层因素为C，则可针对因素C，对所有因素 进行两两比较，得到数值 。

记 ，则A为因素 相应于上一层因素C的判断矩阵。

④各级指标权重的计算

记A的最大特征值为 ，属于 的标准化的特征向量为 ，则 给出了因素 相应于因素C的按重要或偏好程度的一个排序。对于判断矩阵的最大特征根和相应的特征向量，一般采用近似计算，主要有方根法和和积法。

⑤求同一层次上的组合权系数

设当前层次上的因素为 ，相关的上一层因素为 ，则对每一个 ，由④可求得一个权向量 。如果已知上一层 个因素的权重分别为 。

如此一层层自上而下求下去，一直到最低层所有因素的权系数（组合权系数）都求出来为止，根据最低层权的分布即可给出一个关于各方案优先程度的排序。

⑥一致性检验

归一化处理数据后，进一步检验所得到的权重系数是否符合逻辑。常用一致性指数（CI）检验，一般认为CI<0.10时，即可接受专家给定的指标权重。公式如下：

判断矩阵的一致性指标CI与同阶平均随机一致性指标RI之比，称为随机一致性比率。通常要求CR小于0.10，此时可以认为判断矩阵具有满意的一致性，否则需要对判断矩阵进行调整。

3.2灰色关联度分析

3.2.1 灰色关联度的含义

灰色关联度是灰色数学中的一种方法，用来研究事物相互关联、相互作用的复杂因素的影响作用，确定影响事物的本质因素，各种影响因素之间的“灰色”关系清晰化。关联度是事物之间、因素之间关联性大小的量度。

3.2.2关联度的计算

①原始数据的处理

由于各因素各有不同的计量单位，因而原始数据存在量纲和数量级上的差异，不同的量纲和数量级不便于比较，或者比较时难以得出正确结论。因此，在计算关联度之前，通常要对原始数据进行无量纲化处理。其方法包括初值化、均值化等。

1）初值化。即用同一数列的第一个数据去除后面的所有数据，得到一个各个数据相对于第一个数据的倍数数列，即初值化数列。

2）均值化。先分别求出各个原始数列的平均数，再用数列的所有数据除以该数列的平均数，就得到一个各个数据相对于其平均数的倍数数列，即均值化数列。

②计算关联系数

设经过数据处理后的参考数列为：

与参考数列作关联程度比较的p个数列(常称为比较数列)为：

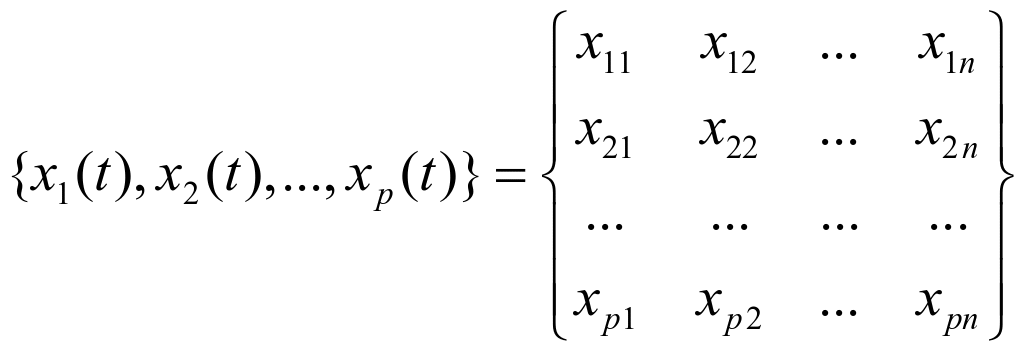
上式中，n为数列的数据长度，即数据的个数。

从几何角度看，关联程度实质上是参考数列与比较数列曲线形状的相似程度。 凡比较数列与参考数列的曲线形状接近，则两者间的关联度较大；反之，如果曲线形状相差较大，则两者间的关联度较小。 因此，可用曲线间的差值大小作为关联度的衡量标准。将第k个比较数列(k＝1，2，…，p)各期的数值与参考数列对应期的差值的绝对值记为：

对于第k个比较数列，分别记n个 中的最小数和最大数为 和 。 对p个比较数列 ，又记p个 中的最小者为 ，p 个 中的最大者为 。 这样 和 分别是所有p个比较数列在各期的绝对差值中的最小者和最大者。

可见，关联系数反映了两个数列在某一时期的紧密程度。 例如，在使 的时期， ，关联系数最大；而在使 的时期，关联系数最小。由此可知，关联系数变化范围为 。

显然，当参考数列的长度为n时，由p个比较数列共可计算出 个关联系数。

③求关联度

由于每个比较数列与参考数列的关联程度是通过n个关联系数来反映的，关联信息分散，不便于从整体上进行比较。 因此，有必要对关联信息作集中处理。 而求平均值便是一种信息集中的方式。 即用比较数列与参考数列各个时期的关联系数之平均值来定量反映这两个数列的关联程度。

不难看出，关联度与比较数列、参考数列及其长度有关。而且，原始数据的无量纲化方法和分辩系数的选取不同，关联度也会有变化。

④排关联度

由上述分析可见，关联度只是因素间关联性比较的量度，只能衡量因素间密切程度的相对大小， 其数值的绝对大小常常意义不大，关键是反映各个比较数列与同一参考数列的关联度哪个大哪个小。当比较数列有p个时，相应的关联度就有p个。按其数值的大小顺序排列，便组成关联序。 它反映了各比较数列对于同一参考数列的“主次”、“优劣”关系。

3.3模糊聚类分析法

3.3.1聚类分析法的含义

聚类分析法又称群分析法，是对多个样本（或指标）进行定量分析的一种多元统计分析方法。样本聚类分析的结果可由聚类图展示出来。

3.3.2模糊聚类法的实施步骤

常用的模糊聚类分析法有基于相似性关系和模糊关系的方法、基于模糊等价关系的传递闭包、基于模糊图论的最大树法、基于目标函数的算法等。本文介绍基于模糊等价关系的传递闭包法进行模糊聚类。

1. 数据标准化

设 是n个待分类的样本点，每个样本可由m 个变量指标来刻画，即

。以每个样本向量为行向量形成如下原始数据矩阵：

利用 空间的闵氏距离可以刻画不同样本点之间的相似程度。若不同指标的量纲不同或指标值变异范围相差悬殊，则需要在计算样本的相似度之前，利用极差变换对数据进行标准化处理，对于两个样本类 和 ，为了判断它们能否各自聚为一类，选用类平均法来进行类间的相似性度量。

2. 模糊聚类分析

根据样本矩阵 构造模糊相似矩阵 这里 表示样本 ， 间的相似程度。显然， ， 。由于模糊相似矩阵只具有自反性和对称性，不满足传递性，我们需要改造相似关系为等价关系。运用平方法求模糊相似矩阵R 的传递闭包，令 ， ，…，直到 ，即求得模糊等价矩阵 。这里“ ”表示“ ”最小值或“ ”最大值运算。对任意的 ，生成模糊等价矩阵 的 截矩阵，将模糊等价矩阵转化为等价的 截矩阵，即布尔矩阵，可以得到有限论域上的普通等价关系，等价关系是可以分类的。当 变动时，由 可以得到不同的分类。事实上，当 且 时， 所决定的分类中的每一个类是 所决定的分类中的某个子集，即 的分类是 的分类的加细；当 从1递减变化到0时， 的分类由细变粗，逐渐归并，形成一个动态的聚类图。

3. 模糊综合排序算法

基于模糊聚类方法，我们能够依据多个指标、多个单位，建立一个分类测评的综合指标体系，对研究的对象进行综合评价。下面给出基于模糊聚类的综合排序算法。

第1步：利用极差变换 将原始数据标准化，得到矩阵

第2步：将标准化后的数据矩阵增加一行指标值全为1的样本，记其样本编号为0。根据公式计算样本 和 之间的相似程度 ，构造模糊相似矩阵 ；再利用平方法求出模糊相似矩阵 的传递闭包，即模糊等价矩阵。

第3步：根据模糊等价矩阵中不重复的元素值确定 的取值集合。根据分类要求，选取合适的 ，利用公式 将模糊等价矩阵转化为等价的布尔矩阵 进行分类，其中 的每行代表一类，取值为1的位置代表对应样本属于该类。让 递减变化得到分类由细到粗的动态聚类过程，则按照与0（样本）归并的先后顺序对其进行排序。

3.4模型的选取

由于灰色理论对长期预测和波动性较大数据列的拟合效果较差，模糊数学定权存在主观因素的问题，影响模型精度，故本文选择层次分析法来进行学习能力综合评价模型的构建。

4.数据收集

4.1指标选取

学习能力，是指学生对学习材料、技能技巧和外界信息的认知、模仿、吸收、编码、储存、整合、优化、提取、使用和创新的能力和本领。综合分析认为，学习能力的要素包括: 其一，动力系统；其二，行为系统；其三，调节系统; 其四，环境支持系统。

4.2指标说明

4.2.1动力系统

动力系统是大学生学习的驱动力所在，本文主要从六个方面进行衡量：①学习定位。②学习态度。③学习动机。④学习毅力。⑤学习兴趣。⑥学习情感。

4.2.2行为系统

行为系统是大学生学习的硬实力所在，本文主要从十一个方面进行衡量，鉴于层次分析法的使用，又将这十一个方面归类为三个大方面：①知识输入。②知识加工。③知识输出。

4.2.3调节系统

调节系统是大学生学习能够持续高效的关键，本文主要从五个方面进行衡量：①学习的自我评价。②自我监控。③学习的方法策略。④学习规划。⑤学习效率。

4.2.4环境支持系统

环境支持系统是影响大学生学习能力的外界环境因素，本文主要从三个方面进行衡量：①学习条件。②学习氛围。③学习奖惩制度。

4.3原始数据的收集

根据大学生综合学习指标评价体系结构图设计问卷（问卷见附录），不同指标进行两两比较，共计进行52次比较。问卷共计收回34份，剔除无效样本4份，有效样本共30份。

5.数据分析过程

5.1 构建层次结构模型

层次结构模型是指分析系统中各因素的逻辑归属及重要性级别进行分层排列，进而形成的一个自上而下的梯阶层次结构。此处目标层是大学生学习能力评价指标，下含一级指标（4个）、二级指标（17个）和三级指标（11个）。将目标层与各级指标层连接起来，就构成了层次结构模型。

5.2构建判断矩阵

本文采用平均法求各大指标体系的判断矩阵，结果如下表。

表 1 二级指标“知识输入”下的3个三级指标的比较

表 2 二级指标“知识加工”下的4个三级指标的比较

表 3 二级指标“知识输出”下的4个三级指标的比较

5.3计算各评价指标权重并赋值

将专家的两两打分，利用方根法计算可以获得每位专家对每层评价指标的权重系数 。公式如下：

对几何均数 进行归一化处理，得到该专家的权重系数打分 ，公式如下：

表 4 每层评价指标的权重系数

5.4一致性检验

归一化处理数据后，进一步检验所得到的权重系数是否符合逻辑。常用一致性指数（CI）检验，一般认为CI<0.10时，即可接受专家给定的指标权重。

经计算，每个指标体系的CR如表

表 5 每个指标体系的CR

结论：CR小于0.10，判断矩阵合理，接受权重系数打分。

5.5确定大学生学习能力评价指标权重

将专家对评价指标打分的权重系数进行算数平均，得出大学生学习能力的综合评价权重表如下：

表 6 大学生学习能力的综合评价权重表

6.结论分析

本文根据构建的大学生综合学习能力评价体系，采用5标度层次分析法，研究评价指标的权重。调查结果显示，在四大评价系统中，动力系统是权重最高的，充分说明了动力系统是学习的源动力，而在动力系统评价体系中，学习定位的权重又是最高的，说明了树立一个好的学习目标的重要性。由图3可知除了环境支持系统外，各大系统的指标权重占比大小按顺序依次排列。本模型为智能学习规划平台的搭建提供了模型依据。

参考文献

[1]李远.大学生数字化学习能力现状调查研究[D].浙江师范大学,2014.

[2]魏萍.论大学生学习力[J].黑龙江高教研究,2014(11):10-13.

[3]李清平.试论信息时代大学生学习能力的构成及其影响因素[J].法制与社会,2008(33):316.

[4]杨宁.大学生深度学习能力的现状调查与提升策略[J].长春教育学院学报,2018,34(02):30-36.

[5]林国耀,连榕.大学生学习能力量表的编制[J].遵义师范学院学报,2009,11(05):52-55.

[6]司开林.学习能力:大学生的源能量[J].常州工程职业技术学院高职研究,2013(04):13-16.

11