云南省保山曙光学校
一、教学内容及分析
(一)教学内容
(二)内容分析
本节课的内容反比例函数的定义指的是形如 (k是常数,k≠0)的函数,其核心是根据具体情境中的数量关系,分析其中的两个变量是否成反比例关系,理解它的关键就是要理解:若两个变量的积一定,那么这两个变量成反比例.学生已经学过对于两个可变的正数,若它们的积一定,当一个变量增大而另一个变量随之减小时,它们就成反比例,本节课的内容反比例函数的定义就是在此基础上的发展.由于它还与其他函数有紧密的联系,所以在本学科有重要的地位,并有总结学习方法的作用,是本学科中函数的重要内容.教学的重点是反比例函数的概念及解析式,解决重点的关键是利用类比学习正比例函数的方法来学习反比例函数.
(k是常数,k≠0)的函数,其核心是根据具体情境中的数量关系,分析其中的两个变量是否成反比例关系,理解它的关键就是要理解:若两个变量的积一定,那么这两个变量成反比例.学生已经学过对于两个可变的正数,若它们的积一定,当一个变量增大而另一个变量随之减小时,它们就成反比例,本节课的内容反比例函数的定义就是在此基础上的发展.由于它还与其他函数有紧密的联系,所以在本学科有重要的地位,并有总结学习方法的作用,是本学科中函数的重要内容.教学的重点是反比例函数的概念及解析式,解决重点的关键是利用类比学习正比例函数的方法来学习反比例函数.
二、教学目标及分析
(一)教学目标
1.了解反比例函数.
2.会求反比例函数的解析式.
(二)目标分析
1.了解反比例函数,就是指通过分析两个变量之间的关系,会判断两个变量是否成反比例关系,是否满足反比例函数的概念,进而确定它们是否为反比例函数.
2.会求反比例函数的解析式就是指结合具体情境体会反比例函数的意义,能根据已知条件确定反比例函数表达式.
三、问题诊断分析
在本节课的教学中,学生可能遇到的困难是理解反比例函数的定义,产生这一困难的原因是反比例函数的概念比较抽象.要解决这一困难,就要在学习反比例函数概念的过程中,充分利用学生已有的生活经验和背景知识,创设丰富的现实情境,引导学生关注问题中变量的相依关系及变化规律,并逐步加深理解.其中关键是在活动中,教师应注意提供思考或研究问题的方向.
四、教学支持条件分析
学生学习本节内容,需在学生掌握了函数与正比例函数的相关知识的基础上才能更好地完成,所以应在学习本章之前让学生先复习以前学过的函数知识,以便能更好地承上启下地学习反比例函数知识,所以本节课宜采用多媒体进行教学.
五、教学过程设计
(一)教学基本流程
概念的引入→概念的形成→概念的辨析→概念的巩固应用
(二)教学情境
问题一:什么是反比例函数?
设计意图:通过已有的经验和知识列出一系列函数解析式,研究这些函数解析式的共同点,类比正比例函数的定义,得到反比例函数的定义,并研究反比例函数的自变量取值范围.
1.概念的引入
问题1:下列问题中,变量间的对应关系可用怎样的函数解析式来表示?
(1)某住宅小区要种植一个面积为1000m2的矩形草坪,草坪的长 (单位:m)随宽
(单位:m)随宽 (单位:m)的变化而变化,请写出
(单位:m)的变化而变化,请写出 与
与 之间的关系式:
之间的关系式:
请根据关系式 填写下列表格:
填写下列表格:
x(单位:m) | … | 5 | 10 | 20 | 40 | 50 | … |
y(单位:m) | … | | | | | | … |
师生活动:
追问1:在这个变化过程中,有几个变量?几个常量?它们分别是谁?
答:在这个变化过程中,有 个变量,它们分别是 ,自变量是 ,因变量是 ,有 个常量,它是 .
追问2:在这个关系式中,y是x的函数吗?为什么?
答:在这个关系式中,y (填“是”或“不是”) x函数关系式,因为在 一定的情况下,当x变化,y也跟着 了,x取一个固定值时,y有 与其对应,即当宽x增大,长y随之 ,所以y x的函数.
(2)京沪线铁路全程为1463 km,某次列车的平均速度v(单位:km/h)随此次列车的全程运行时间t(单位:h)的变化而变化,请写出 与
与 之间的关系式:
之间的关系式:
(3)已知北京市的总面积为1.68×104平方千米,人均占有的土地面积S(单位:平方千米/人)随全市总人口n(单位:人)的变化而变化,请写出 与
与 之间的关系式:
之间的关系式:
师生活动:
请你针对你列出的(2)(3)中的关系式,讨论下列问题:
(1)在这个变化过程中,有几个变量?几个常量?它们分别是谁?
(2)那么这两个关系式是函数关系式吗?为什么?
2.概念的形成
问题2:这三个函数解析式有什么共同点?具有这些共同点的函数解析式就是反比例函数,请根据这些共同点归纳反比例函数的定义?
师生活动:
(1)达成共识后,引导学生归纳反比例函数的概念:一般地,形如 (k是常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数.
(k是常数,k≠0)的函数称为反比例函数,其中x是自变量,y是函数.
(2)若m是n的反比例函数,那么怎么表达这个反比例函数?若a是b的反比例函数,那么怎么表达这个反比例函数?
(3)请你任意说出一个比例系数,并指定一位同学来说出对应的反比例函数.
(4)请学生举例说明生活中存在的反比例关系.
讨论:这个反比例函数关系式 还有其它形式吗?
还有其它形式吗?
3.概念的辨析
例1. 下列关系式中,y是x的反比例函数的是 ?并指出相应k的值?
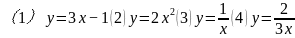

设计意图:加深学生对反比例函数几种表达式的认识.
变式练习:在下列函数中,y是x的反比例函数的是( )

例2.当m为何值时,函数 是反比例函数?
是反比例函数?
解:由题意可得:



设计意图:掌握反比例函数的其它表达形式,针对 明白两个地方:其一反比例系数k不能为0,其二自变量x的指数为
明白两个地方:其一反比例系数k不能为0,其二自变量x的指数为 .
.
变式练习:已知 是反比例函数,则m的值为多少?
是反比例函数,则m的值为多少?
4.概念的巩固与应用
问题二:如何求反比例函数表达式?
设计意图:明确初中阶段求函数解析式一般可以用待定系数法来求解.
例3:已知y是x的反比例函数,当x=2时,y=6.
(1)求出y与x的函数关系式;
(2)当x=4时,求y的值.
设计意图:通过类比用待定系数法求正比例函数解析式的方法求反比例函数解析式.
师生活动:教师提出问题,学生独立思考,解答问题,教师引导学生理解“y是x的反比例函数”这句话的意义,总结得出求反比例函数的方法,然后由学生自主解答,请学生代表到黑板上解答,并纠正核对.
解:(1)设y与x的反比例函数的解析式为 ,
,
将x=2,y=6代入上式得
解得k=12
∴y与x的反比例函数的解析式为
(2)当x=4时
变式练习:已知点(2,-7)在反比例函数 的图像上,那么k为何值?
的图像上,那么k为何值?
课堂小结
1.通过这节课的学习你有哪些收获?
2.请你总结初中阶段学习函数的步骤?
3