向量姊妹式与三角形的“心”缘

向量姊妹式与三角形的“心”缘

熊有胜

湖北省十堰市房县第一中学 442100

在近几年的各级各类考试中，经常出现向量的结构式与三角形的心（重心、垂心、外心、内心）相关联的问题，然而这些向量式子貌合却神离，考生常出现把握不住的现象。下面选择几例予以破析，旨在探索题型解决方法。

例1、已知O是 所在平面内的一点，若

（1） + + = ，则O为 的 心；

（2）a +b +c = (a、b、c分别为 的角A、B、C所对的边)，则O为 的 心。

分 析：要确定O是 的重心、垂心、外心还是内心，应首先明确这些概念的含义，即看O在 的某边的中线上、高线上、中垂线上还是某个内角的平分线上。

（1） + + = =－（ + ）

如图①，以OA、OC为邻边作 ，则

= + =－

设AC交OD于点E，则 = 、

BE是 的AC边上的中线，且

O为 的重心

（2） a +b +c = ， ， ，

（a+b+c） +b

即 .

与 分别为与 和 方向相同的单位向量，

设 = ， = ， ，则

四边形ADPE为平行四边形，又 = ，所以四边形ADPE为菱形，

所以AP平分 ，而 = ，

故 、 共线，即AO平分 ，

同理可证：BO平分 ，CO平分 ，从而O是 的内心。

评注：有关已知向量的和、差结构的式子，常用平行四边形法则进行破析，同时注意线段中点的应用。

例2、已知O是 所在平面内的一点，若

（1） ，则O是 的 心；

（2） ，则O是 的 心；

（3） =0，则O是 的 心。

分析：（1）

即 ，所以则O是 的外心

（2）由 知， ，

即 ， ，故O在AC边的高线上，

同理可证：O也在AB边和BC边的高线上，所以O是 的垂心。

（3） 与 = （E在 的外角平分线上）垂直，所以O在 的内角平分线上，同理：O在 的内角平分线上，故O是 的内心。

评注：关于数量积的已知条件，要恰当应用数量积的运算律，对结构式子进行变形，注意非零向量垂直的充要条件的使用。

例3、已知O是 所在平面内的一点，若动点P满足

（1） ，

则动点P的轨迹一定通过 的 心；

(2) ，

则动点P的轨迹一定通过 的 心；

（3） ，

则动点P的轨迹一定通过 的 心；

（4） ，

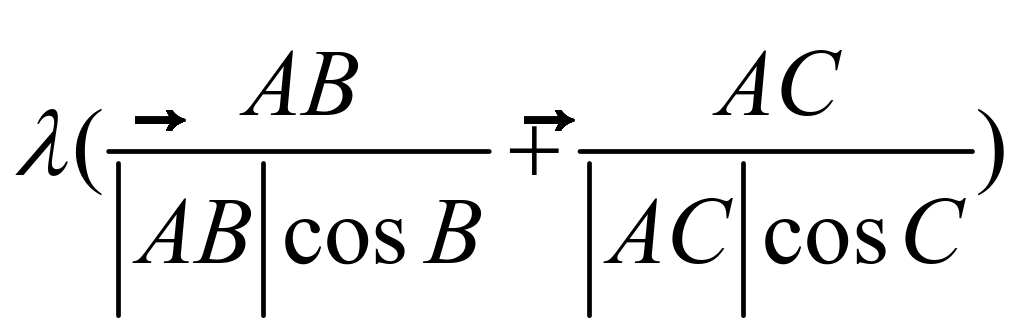则动点P的轨迹一定通过 的 心。

分析：（1）由 ，得 = ，

设BC的中点为E，则 =2 ， =2 ， A、P、E三点共线，而AE是中线，则动点P的轨迹一定通过 的重心。

（2）由例1（2）的分析得，动点P的轨迹一定通过 的内心

（3）由 ，得 = ，

如图②：作 的高AD，则 ，

= ，

由（1）可知动点P的轨迹一定通过 的重心。

（4）所给式子可化为： = ，

= （ ）=0

，即P点在过点A且垂直于BC的直线上，

动点P的轨迹一定通过 的垂心。

评注：这种类型的问题较为灵活，要综合运用向量运算的法则、运算律及垂直充要条件等。所以重在观察和积累才能做到万无一失。