山西师范大学数学与计算机科学学院 山西省临汾市 041000
摘要:本文主要针对高压油管的压力控制以及喷油量稳定问题进行了相关研究,通过建立目标规划模型,利用高压油管内压力随时间的变化来展示所得结果的合理性。首先高压油泵在A处压力是不变的,单向阀开关会控制供油时间的长短,然后和喷出的油量一起来影响高压油管内的压力。其次燃油流量,与极径与极角有关系,从阀门进入的油量,与凸轮柱塞腔和油管的压力之差有关系,喷油管喷出的燃油量与高压油管内部的压力有关系,高压油管的压力由进入和喷出的燃油量共同决定,也就是燃油的变化量所决定。最后再增加一个喷油嘴,每个喷嘴喷油规律相同,再安装一个减压阀,给出减压阀开启时间,看看到底什么时候才能使压力保持稳定,然后拟合,通过运行代码,来计算出最优的结果。
关键词:目标规划 喷油管 减压阀 拟合
引言
给出的喷油器工作次数、高压油管尺寸和初始压力的情况下,得出确定凸轮的角速度,整个过程中,高压油管内的压力尽量稳定在100 MPa左右。在此基础下,添加一个完全相同的喷油嘴,包括规律也一样,那么请问应该如何调整喷油和供油的策略?现假设在D处安装一个单向减压阀,其是出口直径为 =1.4mm的圆,打开后在压力的作用下,高压油管内的燃油可以回流到外部低压油路中,从而使高压油管内燃油的压力减小,应该如何设计油泵和减压阀的控制。
=1.4mm的圆,打开后在压力的作用下,高压油管内的燃油可以回流到外部低压油路中,从而使高压油管内燃油的压力减小,应该如何设计油泵和减压阀的控制。
1、问题分析
首先单向阀开启燃油进入和喷油器燃油喷出都为变量,所以需要控制燃油的进入量和喷油嘴喷出来的油量来使高压油管内部压力(100 Mpa)保持不变,若要满足就需要燃油进入总量与喷出总量一致。其次将高压油管内的压力从100 MPa增加到150 MPa,且分别经过不同时间的调整过程后稳定在150 MPa,应该如何调整单向阀的开启时长。最后再增加一个喷油嘴,每个喷嘴喷油规律相同,所以两个喷油嘴的喷油速率一致,但不知道的是两个喷油嘴开启时间差。为了更有效地控制高压油管的压力,现计划在D处安装一个单向减压阀。给出高压油泵和减压阀的控制方案。
2、模型的建立与求解
喷油嘴每秒工作10次,每次工作时喷油时间为2.4ms,因此喷油嘴的周期
 =1/10s=100ms。
=1/10s=100ms。
而喷油的时间为0.24ms,在一个周期内,喷油的总流量:

高压油管的体积为:

算出B口流出的燃油的质量 ,可以得到2.4ms , B口流出的燃油量2.4ms内的喷油速率与时间所围成的面积,即梯形的面积,即2.4s内B口流出的燃油量为: 44
,可以得到2.4ms , B口流出的燃油量2.4ms内的喷油速率与时间所围成的面积,即梯形的面积,即2.4s内B口流出的燃油量为: 44 。根据题目要求要将高压油管内的压力尽可能稳定在100MPa左右,那么也就是说,当压力|为100 MPa时,燃油的密度为0.850 mg/
。根据题目要求要将高压油管内的压力尽可能稳定在100MPa左右,那么也就是说,当压力|为100 MPa时,燃油的密度为0.850 mg/ 可以根据质量公式计算出2.4s内B口流出的燃油的质量
可以根据质量公式计算出2.4s内B口流出的燃油的质量

依据弹性模量与压力的关系,可以看出当压力为100Mpa时,弹性模量为2171.4Mpa,根据燃油的压力变化量与密度变化量成正比,且比例系数E/P,可以得到并且计算出A口加入的高压侧燃油中燃料的密度为:.0.8711mg/ ,进高压油管的流量为
,进高压油管的流量为

管截面面积为0.49pi。那么根据公式V=Qt进出高压油管中燃料的体积为

要使得高压油管内的压力尽可能维持在100MPa左右,所以就要保持一个周期内,从A口进入的质量和从B口喷出去的质量一样。带入公式算出t=0.28ms.在一个周期内,开启A阀门的时间是0.28ms, 关闭的时间是99.72ms。
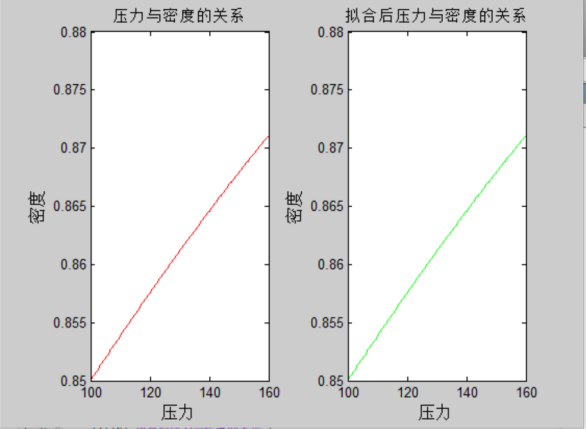
图1 压力与密度关系图
可以看出,压力和密度大致呈现呈线性关系,拟合度0.99.现在要求压力不变,就是要求质量不变,那么建立最小值的目标函数

得出t=0.4左右,偏差较大,重新建立一个最小值目标函数,

解出t=0.291在实际工作过程中,高压油泵的柱塞腔出口为高压油管A处提供燃油,喷油嘴的针阀控制喷油的喷油嘴喷出。每一个极角,对应一个极径,然后影响凸轮的转动,进而影响压缩体积,然后影响压力,再作用于阀门。
图2 凸轮的示意图。

凸轮上升的程度是 则体积为
则体积为


由密度与压力的关系式,得出0.5Mpa时的密度为0.8154.

下止位点,腔内的燃油质量时 上止位点时,
上止位点时,

据推测,此时压力应该为100Mpa.

燃油喷出。拟合喷油时间与针阀的升程的关系得到


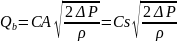
目标函数:

添加一个完全相同的喷油嘴,包括规律也一样,现假设在D处安装一个单向减压阀,其是出口直径为 =1.4mm的圆,打开后在压力的作用下,高压油管内的燃油可以回流到外部低压油路中,从而使高压油管内燃油的压力减小,依据进油依旧是由凸轮的角速度决定,假设两个喷油嘴的喷油规律一样,周期还是100ms,假设两个喷油嘴相差
=1.4mm的圆,打开后在压力的作用下,高压油管内的燃油可以回流到外部低压油路中,从而使高压油管内燃油的压力减小,依据进油依旧是由凸轮的角速度决定,假设两个喷油嘴的喷油规律一样,周期还是100ms,假设两个喷油嘴相差 喷出。
喷出。
参 考 文 献
[1]李海洋,杨海涛,张清林,杨翔宇,陈大陆,共轨系统燃油压力及物性参数测试研究现代车用动力。
[2]丁同仁,李承治,常微分方程。
2