(江苏第二师范学院 江苏 南京 211200 )
摘要:回流焊工艺是实现表面组装不可缺少的一个环节,回焊炉内加热环境的设定会影响电子元件的焊接质量。对于给定的参数规格的回焊炉,本文通过建立微分方程模型,研究回焊炉的炉温曲线,最后通过优化模型得出最优炉温曲线。通过分析回焊炉内的传热模型特点,将炉内温度传递方向视为垂直于上下温区,基于傅里叶热传导定律和牛顿冷却定律,在时间和空间上取微元建立一维偏微分方程,研究炉内的非稳态传热过程,并运用数学物理方法以及Matlab对方程化简求解,得到暂态阶段的温度场函数U(y,t)。
关键词:非稳态热传导方程 有限差分法 追赶法 目标优化模型
科技飞速发展的背景下,电子产品进一步轻薄话、微型化,这对组装工艺焊接技术有了更严格的要求,既要避免因温度过高导致元件损坏,又要避免因温度不足导致焊接不牢固,因此,合理设定回焊炉内的加热环境是保障电子元件焊接质量的前提,这就要求我们控制相关参数,提供合适的炉温,设置合理的传送带过炉速度,进一步优化炉温曲线。
根据回焊炉内各温区设定的温度,通过热传导方程和牛顿冷却定律,建立一个非稳态热传导方程模型,得到不同时间和空间处的温度分布,综合考虑电子元件在不同位置的温度,运用温度的连续性找到初始和边界条件,建立热传导和对流传热模型。通过热传导和对流传热模型建立参数与焊接区域中心温度的关系,最后,查阅资料并利用MATLAB遍历求解得到参数 的值。
的值。
在回焊炉对电子元件加热的过程中,热量主要以热风对流传热为主,并且伴随热传导,本文我们忽略了传热而过程的热辐射,通过热传导公式和牛顿冷却定律建立非稳态偏微分传热对流模型。
1.1 牛顿冷却定律
牛顿冷却定律不仅适用于温度高的物体向温度低的物体传递热量的过程,也适用于温度较低的物体吸收热量逐渐升温的过程。
炉内加热区域的温度向焊接区域边界传递的方式是热对流,为了计算方便,将牛顿冷却定律的表达式转化为微分形式:
 (1)
(1)
其中,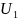 为元器件表面的温度,
为元器件表面的温度,  是传送带上的温度,
是传送带上的温度,  为传热系数。
为传热系数。
回焊炉内传送带上温度的分布与x、 、
、 、
、 和
和 有关,通过对传送带上各部分温度的分布数据进行拟合,根据牛顿冷却公式,可得到传送带上温度分布
有关,通过对传送带上各部分温度的分布数据进行拟合,根据牛顿冷却公式,可得到传送带上温度分布 。
。
1.2 热传导公式
热传导是因为导体内部存在温差,引起自由电子移动的结果,回焊炉炉温满足热传导方程,并且满足一定的初始和边界条件,其中,三维热传导方程满足:
 (2)
(2)
其中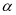 为热扩散率,
为热扩散率, 为比热容,
为比热容,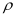 为密度;
为密度; 表示温度随时间的变化,
表示温度随时间的变化, 、
、 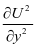 和
和 表示温度随空间的变化;
表示温度随空间的变化; 表示内部热源的影响。
表示内部热源的影响。
由于电子元件不含内部热源,并且为了简化模型,对比电子元件将回焊炉视为无限大,下面只考虑电子元件的厚度,于是式(2)的三维模型简化为一维模型:
 (3)
(3)
1.3 初值和边界条件以及模型的建立
在整个回焊炉传热模型中,两小温区之间存在间隙(单位:cm),间隙两端为第一类边界条件,问题转化为满足如下初始边值条件的一维微分方程模型:(对于焊接区域的温度变化规律,根据热传导公式和牛顿冷却定律,建立一阶偏微分方程,确定初值和边界条件,得到焊接区域温度变化的非稳态偏微分传热对流模型。模型中热传导的系数 和热对流的系数
和热对流的系数 未知,通过Matlab对系数进行遍历求解,得到最优传热对流系数,拟合出最优炉温曲线。)
未知,通过Matlab对系数进行遍历求解,得到最优传热对流系数,拟合出最优炉温曲线。)
 (4)
(4)
令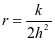 ,代入上述(2)式,用显式差分格式对热传导模型进行离散得:
,代入上述(2)式,用显式差分格式对热传导模型进行离散得:
 (5)
(5)
根据方程(4),结合上述离散化方程,得出以下矩阵:
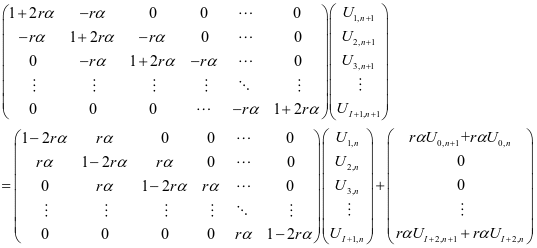 (6)
(6)
再利用MATLAB对(5)式进行遍历求解。
1. 假设回焊炉内的空气为理想气体,不考虑温度对空气比热容的影响;
2. 假设空气为静态,由于回焊炉内空气层厚度较小,不考虑热辐射;
3. 假设开始加工时回焊炉内空气温度稳定,电子元件温度变化连续;
4. 假设回焊炉内温度传递方向垂直于上下温区,可以将系统假设为一维模型;
5. 假设回焊炉内的热量无损耗;
6. 假设温度相同的小温区内各点温度都相同;
7. 忽略温度、水蒸气对材料热传导率的影响,即视材料的热传导率恒定;
3.1优点
(1) 在解决问题过程中对模型进行简化,便于问题的解决。
(2) 建立了考虑热传导和热扩散的一维非稳态传热模型,考虑问题较为全面(忽略的热辐射对传热过程影响很小)。
3.2缺点
(1)在建立回焊炉炉温模型时,做出了一些假设,忽略了热辐射对系统的影响,同时也忽略了元件氧化对传热的影响,因此具有一定局限性和片面性。
(2)利用有限差分法计算的温度场可能存在部分数值误差。
利用Crank-Nicolson差分格式对模型进行求解,计算量小且效率较高。
作者简介:张婧(1999—),女,汉族,本科,江苏第二师范学院,研究方向:数学模型。
[1] 汤宗健,谢炳堂,梁革英. 回流焊炉温曲线的管控分析 [J].电子质量. 2020.08.20
[2] Fadugba S.E.,Edogbanya O.H,Zelibe S.C.”Crank Nicolson method for solving parabolic partial differential equations”[J],IJA2M,2013,1(3):8-23.
[3] 靳涛. 高温作业专用服装的温度分布模型[J].消防界.2020.05.27
[4] 杨世铭,陶文栓.传热学[M].第四版,北京:高等教育出版社,(2006)
[5] 姜启源,谢金星,叶俊. 数学模型[M]. 第五版,北京:高等教育出版社,2018.5.