浅议初中数学配方思想的教学及应用

浅议初中数学配方思想的教学及应用

张云兵

朝天区之江初级中学

【摘要】 配方思想是被应用于解决数学问题的一种常见的数学思想，是比较基础的。它的解题技巧性较强，应用十分广泛，是学生学好数学的关键。

关键词： 配方思想 解题技巧 教学 应用

数学学习就是教会学生数学思维，数学思想和方法，能用数学思想、方法和相关的数学知识去解决生活中的实际问题。而数学思想又蕴涵在数学知识形成、发展和应用的过程中，是数学知识和方法更高层次上的抽象与概括。在初中阶段的数学教学中，配方思想是被应用于解决数学问题的一种常见的数学思想。是比较基础的，它是其他数学问题解决的关键所在。利用配方法解题是初中生必须掌握的一种重要的解题方法。只有掌握了这种最基础的数学思想方法，才能为后续的新知做好铺垫，也才可能学好数学这门学科。

现结合我的教学，谈谈配方思想的教学及应用。

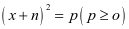首先，重视配方思想的教学，了解配方在初中教学内容中的应用。在教学时才能对学生进行适时深入的渗透。配方主要出现在八年级上册《整式的乘除》和八年级下册《二次根式》,以及九年级上册《一元二次方程》、《二次函数》（人教版）等章节。比如配方思想在《一元二方程》中的呈现：在一元二次方程的解法中，教材先讲了直接开平方法，也就是只要方程可化为 或 的形式，都可根据平方根的意义，通过直接开平方法得到方程的解。在此基础上再讲配方法解一元二次方程。教科书安排了“探究”栏目，思考怎样解方程 ，自然就要引导学生如何才能将方程变成 ，这样就需要把常数项移到方程的右边，未知项放到方程的左边。然后将左边配方，变成一个完全平方式就可以了。这样就得到了配方法解一元二次方程的步骤和解法。在此基础上，教材有安排了“探究”栏目，引导学生自主地用配方法解一般形式的一元二次方程 ，得到公式法的求根公式。所以只有知晓配方思想所出现的章节内容，呈现的方式，教学才能胸有成竹，才能在教学时适时渗透配方思想。在这部分内容的教学过程中学生又总是难以掌握。只有通过多次反复的练习、思考、引导，和学生长时间的积累，才可使学生逐步感悟配方思想，并学会配方。如果学生掌握了配方的思想，就有助于学习新的数学知识，也可以使复杂的数学问题变得更加简单，容易解决。从而增强学生学习兴趣。

第二，要知道什么叫配方，掌握式子的结构特征，才能正确配方。配方就是把一个式子或一个式子的某一部分化成完全平方式或几个完全平方式的和、差形式。它是最常见的恒等式变形。首先要掌握完全平方公式： 它的特征是：①左边有三项；②有两项可以表示成一个数或一个式的平方且符号相同，还有一项是平方项底数积的2倍。③右边是两平方项底数的和（或差）的平方。是和是差的完全平方，关键是看积的2倍的符号。其次掌握配方的基本形式①_，②_，③_{。只要掌握了完全平方式的特征，结构特点，以及配方常见的形式，配方就会得心应手。}

第三，要知道配方法的题型及呈现方式,才能对症施药，引导学生正确解答，形成和掌握配方思想的解题技巧。配方主要应用于代数式的化简、求值、计算、解不等式（组）和方程（组）的证明及求函数的最大值、最小值等问题。

下面简单谈谈配方法在初中各章节的一些应用

（一）、用于二次根式的化简

例1：计算的值

_{分析：如果}能化成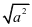形式就可以化简求值，因此只需根号下是一个完全平方式即可，根据完全平方式就需要将拆成三项，找到公式里的，而_，所以

练习：计算的值（ ）

A.1 B. C. D.5

这类二次根式的化简求值题，在竞赛题中较多。往往需要将二次根式转化为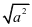 的形式，因此需要将根号下的式子化成一个完全平方式。在教学时应反复强化思路，多举例，使学生形成定向思维。

（二）、用于求代数式的值

例2．已知 ，求代数式 的值

分析：求 的值，只需知道字母 和 的值，而题中没有告知，故需两个关于 和 方程。因此原方程 需变形处理。而方程中 配上常数项9，就可以构成完全平方式 ； 配上常数项25，就可以构成完全平方式 ，式子中常数项34刚好可拆成9和25，由此可将式子变形为 ，从而可求出 和 的值，再代入计算即可。

在教学时引导学生观察式子的特征，根据已知条件所给的方程右边为零，这种题往往需利用非负数的和为零，这几个数都为零，故需将方程右边配方，化为几个非负数和为零的形式。再运用几个非负数的和为零性质求出所求字母的值，从而可求出所含字母代数式的值。

练习：1、已知 ，则 ， 。

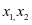2、已知 是方程 的两根，则 的值为 。

（三）解一元二次方程

例3：用配方法解方程

解：化二次项系数为1，得

移项，得

配方，得

整理得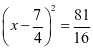

开平方得

用配方法解一元二次方程的一般步骤为：一“化”，即化二次项系数为1；二“移，即把常数项移到方程的右边；三“配”，即在方程两边同时加上一次项系数的平方；四“开”，即方程两边开平方；五“定”，即定解。配方法解一元二次方程的关键就是配方。教学时，就应反复强调。

（四）、用于求最值

1、多项式的最值

例4：代数式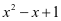 的值（　　）

Ａ．恒为正 Ｂ．恒为负 Ｃ．可能为0 Ｄ．不能确定

解： ，故选A。

说明：在求最大（小）值时的应用是，往往需要利用配方法将原式化成一个完全平方式后即可求出最值。

练习：（1）多项式 的最大值是

（2）当时，求多项式 有最 （大或小）值为 。

2、求二次函数的顶点坐标和函数的最值

对于任何一个二次函数都可以通过配方法把原来的二次函数化成 的形式，则得到顶点坐标（h，k）；若a>0，函数值y有最小值k；若a<0时，函数值y有最大值为k。

例5．写出下列抛物线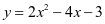 的开口方向、对称轴和顶点坐标及最值：

思路：要求抛物线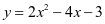 的开口方向、对称轴和顶点坐标及最值，只需通过配方将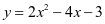_{转化成顶点式的形式即可。}

解：　　

所以，抛物线的开口向上，对称轴为直线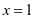 ，顶点坐标是 ，该函数有最小值-5。

练习：1．将二次函数y＝x²－2x＋3化为y＝(x－h)²＋k的形式，结果为（ ）

A．y＝(x＋1)²＋4 B．y＝(x＋1)²＋2 C．y＝(x－1)²＋4 D．y＝(x－1)²＋2

（五）、用于证明

例6：证明x无论取何实数，代数式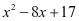 的值恒大于0，

思路：通过配方将二次三项式化为非负数的形式，

证明：∵ = =

又∵

∴ 的值恒大于0，

即对所有实数 ，方程左边的代数式的值均不等于 ，因此，原方程没有实数根．

“配方法”在代数证明中的应用，有些看似乎无从下手，如果用“配方法”将其变成完全平方式后，便“柳暗花明”了。当我们学习了函数后，还会知道“配方法”在二次函数中也有着广泛的应用。

总之，配方思想对于学生学好数学起到了基础而又关键的作用。在教学时适时渗透，引导，并反复练习，使学生掌握并能运用，迅速的解决有关数学问题。

参考资料：

1、《初中数学课程标准》；

2、九年级数学上册《教师教学用书》；

3、《中小学教育》2019年8月1期 作者：郭剑平配方思想在初中数学解题中的应用。