孝感市大悟县黄站中学 邮编: 432824
摘要:随着近些年初中数学课程标准的不断调整和人教版中学教材的逐步改版,弦切角定理、切割线定理和割线定理逐渐远离了大家的视线。但是在很多与圆相关的复杂考题中,它们对于正确快速的解答依然能起到很大作用。就算不再把它们编为必修内容,也可以选修或探究的形式让学生进行了解和学习,以拓宽视野发散思维。
关键词:弦切角定理、切割线定理、割线定理、推理证明、应用。
说起弦切角定理和切割线定理,现在的中学生可能都不知道,因为新的人教版中学数学教科书中早已没有了这两个定理的内容。我们先来回顾一下下面三个定理的具体内容。
1 .弦切角定理:弦切角等于它所夹的弧所对的圆周角。几何语言如下:
.弦切角定理:弦切角等于它所夹的弧所对的圆周角。几何语言如下:
如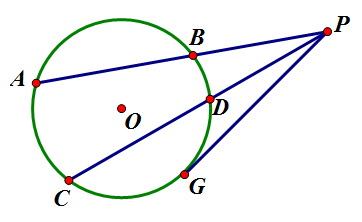 左图所示,若AB是⊙O的切线,BC是⊙O的弦,∠BDC是弧BC所对的圆周角,则∠ABC=∠BDC
左图所示,若AB是⊙O的切线,BC是⊙O的弦,∠BDC是弧BC所对的圆周角,则∠ABC=∠BDC
2.切割线定理:从圆外一点引圆的切线和割线,切线长是这点到割线与圆交点的两条线段长的比例中项。几何语言如下:
如左图所示,若PG与⊙O相切于点G,PD与⊙O相交于C、D两点,则PG2=PC·PD。
3.割线定理:从圆外一点引圆的两条割线,这一点到每条割线与圆的交点的两条线段长的积相等。几何语言如下:
如上图所示,过点P的两条直线分别与⊙O相交于点A、B和点C、D,则PA·PB=PC·PD。
以上三个定理都可以通过圆的相关性质和定理结合三角形相似的性质及定理来推理证明。所以现在的教材虽然把这部分知识删除了,但是如果有关圆的证明推理题中需要用到以上结论时一样可以通过逐步推理证明得出想要的答案。不过也正是因为教材中没再把它们以定理的形式给出,导致每次遇到此类型的考题都要写一次推理过程。例如下题:
例1(孝感市2015年数学中考题)如图,![]() 为⊙
为⊙![]() O的直径,
O的直径,![]() 是
是![]() 延长线上一点,
延长线上一点,![]() 切⊙O于点
切⊙O于点![]() ,
,![]() 是⊙O的弦,
是⊙O的弦,![]() ,垂足为
,垂足为![]() .
.
(1)求证:![]() ;(4分)
;(4分)
(2)过点![]() 作
作![]() 交⊙O于点
交⊙O于点![]() ,交
,交![]() 于点
于点![]() ,
,
 连接
连接![]() .若
.若 ,
,![]() ,求
,求![]() 的长.(6分)
的长.(6分)
本题第(1)问直接就是对弦切角的三种情况之一进行证明,而第(2)问也正好需要用到第(1)问的结论作为已知条件进行解答。第(1)问证明过程如下:
解:连接OC,因为PC切⊙O于点C,所以OC⊥PC,所以∠PCO=90º=∠PCA+∠ACO;因为AB是⊙O的直径,所以∠ACB=90º,又∠ACB=∠ACO+∠OCB,所以∠PCA=∠OCB;因为OC=OB,所以∠OCB=∠OBC=∠ABC,所以∠PCA=∠ABC。
如果以上三个定理能在教材上进行学习然后直接投入使用的话,对很多高难度推理证明题都能简化运算。请看下面这道题:
例 2(孝感市2018年数学中考题)如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
2(孝感市2018年数学中考题)如图,△ABC中,AB=AC,以AB为直径的⊙O交BC于点D,交AC于点E,过点D作DF⊥AC于点F,交AB的延长线于点G.
(1)求证:DF是⊙O的切线;
(2)已知BD=2![]() ,CF=2,求AE和BG的长.
,CF=2,求AE和BG的长.
解析:第(1)问连接AD和OD由AB是直径得出∠ADB=90o,由等腰三角形的性质可以得出AD是∠BAC的平分线,又由OA=OD得出∠OAD=∠ODA,所以∠CAD=∠ODA,所以OD∥AC,得出∠ODG=∠AFG,由DF⊥AC得出∠AFG=90º,所以∠ODG=90º,由此证出DF是⊙O的切线。
而第(2)问,如果使用割线定理,可作如下推理运算:
由(1)知AD垂直且平分BC,得DC=BD=2![]() ,又∠ABD=∠C,所以cos∠C=cos∠ABD,即
,又∠ABD=∠C,所以cos∠C=cos∠ABD,即![]() =
=![]() ,将CF=2和DC=BD=2
,将CF=2和DC=BD=2![]() 代入等式解得AB=10,所以AC=AB=10,由割线定理得CE·AC=CD·CB,且CB=2CD=4
代入等式解得AB=10,所以AC=AB=10,由割线定理得CE·AC=CD·CB,且CB=2CD=4![]() ,解得CE=4,所以AE=AC-CE=6.
,解得CE=4,所以AE=AC-CE=6.
接下来,由题意知EF=CE-CF=2,由∠AEB=90º=∠AFG可得BE∥GF,所以 ,代入各线段的值即可得出BG=
,代入各线段的值即可得出BG= 。不知大家是否觉得这个方法也很巧妙和简单。
。不知大家是否觉得这个方法也很巧妙和简单。
我们再看看下面这道题:
例3(重庆市2018年数学中考题)如图,△ABC中,∠A=30o,点O是边AB上一点,以点O为圆心,以OB为半径作圆,⊙O恰好与AC相切于点D,与AB交于点E,连接BD,若BD平分∠ABC,AD=2 ,求⊙O的半径。
,求⊙O的半径。
 解析:先连接OD,因为⊙O恰好与AC相切于点D,所以OD⊥AC;由OB=OD可知∠OBD=∠ODB,由BD平分∠ABC得∠OBD=∠CBD,所以∠ODB=∠CBD,得出OD∥BC,可得∠C=∠ODA=90o,又已知∠A=300,所以∠ABC=60o,∠ABD=
解析:先连接OD,因为⊙O恰好与AC相切于点D,所以OD⊥AC;由OB=OD可知∠OBD=∠ODB,由BD平分∠ABC得∠OBD=∠CBD,所以∠ODB=∠CBD,得出OD∥BC,可得∠C=∠ODA=90o,又已知∠A=300,所以∠ABC=60o,∠ABD= ∠ABC=300=∠A,这样就可得出BD=AD=2
∠ABC=300=∠A,这样就可得出BD=AD=2 ,由∠CBD=
,由∠CBD= ∠ABC=300得CD=
∠ABC=300得CD= BD=
BD= ,BC=
,BC= =3,所以AB=2BC=6,然后由AD2
=3,所以AB=2BC=6,然后由AD2
=AE·AB,得出AE=2,直径BE=AB-AE=4,所以⊙O的半径为2。
上面这道题如果不使用切割线定理,势必要多作几条辅助线进行几何分析,利用相似证明和加大运算量来达到解题目的,而上面展示的解法可以很好地避免过多的辅助线和相似性推理对考生解答思路的干扰。
近几年因为初中数学课程标准的调整和人教版中学教材的改版,数学中考题中有关圆的推理证明和运算考察的更多的是三角形相似和线段成比例、等量代换等相关知识点的掌握情况。作为常年奋斗在教育最前沿的一线教师,笔者认为与圆相关的等量问题和线段成比例问题是有关圆的推理运算的重点,而弦切角定理、切割线定理和割线定理也是相似性在与圆相关的几何推理证明中的经典结论。这些定理在很多与圆相关的复杂考题中如果用的好,作用还是相当大的。就算不对这三个数学定理当作中学必修内容,也可以列入选修部分,或者以思考探究的形式让学生进行学习,在学生自已证明成功并正确归纳后,可以允许他们在合适的题型中把这些结论以定理的形式进行直接应用。就算大多数题目都不一定能用上这些定理,对它们的推理探究也可以拓宽学生的视野,发散他们的思维,使学生在寻找规律和解决各种类似问题时让他们有更大的思考空间和更多的做题思路。只有宽广的视野和发散的思维才能让学生在各种复杂的问题中有足够多的分析思路,并找出最佳解决方案。