华北理工大学 河北唐山 063200
摘要：数学规划能够为更好地配置资源、组织生产提供理论和方法，其中线性规划是在现代管理中应用范围最广、理论比较完善的一个重要分支，而影子价格则是在线性规划过程中对偶变量的经济含义，可以为生产决策者提供多方面的有效信息，本文对企业在生产过程中，如何合理利用资源取得最大效益进行了探讨，使电子产品加工与运筹学相结合，通过lingo软件，有针对性的进行优化决策，使其效益最大化。
关键词：线性规划；企业决策；资源管理；影子价格
前言：
“运筹帷幄之中，决胜千里之外”是我们耳熟能详的一句古语，运筹学的运筹就是从中提取而来。运筹学以数学理论基础模型为基础，结合管理学相关知识，来解决军事结构、生产计划中的管理决策问题。通过科学可靠的理论系统为决策者提供决策依据，为现实生活中的流程优化、生产计划规划提供了重要理论。在企业生产中，劳动，资本，信息等生产要素对一个企业的生死存亡起到关键性的作用。企业如何能在市场信息下，合理利用运筹学中的理论依据，对劳动人力，现有资源进行合理正确计划调配至关重要。
影子价格概述
2.1影子价格在线性规划模型中的含义
影子价格，又称有效价格，是企业资源配置的重要依据。在内部投产或转让决策中，在企业内部资源的优化过程中，都具有一定的参考价值。下面是影子价格在线性规划模型中表达的具体含义：
原问题
（1）
其对偶问题为
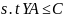
（2）
其中，若线性规划（1）中的问题为最优基是B，则资源i的影子价格yi则是其对偶问题（2）的最优解。由此，在追求总利润最大的目标下，影子价格是在此约束条件下增加一个单位而产生的目标函数最优值的变化量。
而从经济意义上来讲，影子价格不仅表示单位资源或单位产品的机会成本；还可以表示在生产计划中，有效资源配置、产品或服务的边际价格。
2.2影子价格的广泛应用
一般说来,影子价格也可以提供以下几个方面的信息使他在生产决策领域有了更为广泛的应用。
①影子价格可以反应如何配置资源能达到最优的生产方案。
在企业生产生活中，部门之间虽然独自运营，但从企业利润最大化的角度出发，在资源上分配上却相互制约。这样形成的各种约束就形成了相应的线性规划模型，此时，为了企业最优规划，就可以以影子价格为着力点，制定生产计划。
②影子价格可以反应增加资源的合理价格。
影子价格在资源定价上的应用主要表现在可以利用影子价格来分析市场资源供给情况，和自身公司内部资源价格相比较的结果就可以当做增加资源价格的重要依据
③影子价格可以作为决策者考虑新产品的价格的依据。
影子价格在价格变动当面有着其他参数无法比拟的优势，我们可以通过生产产品影子价格和市场上相应产品的价格比较，通过分析其生产产品的经济效应来进行是否投产的决策。
由上述定义，因为影子价格是其线性规划对偶模型的最优解，我们可以根据企业的目标建立相应的线性规划模型，然后将原线性规划问题转化为它的对偶问题,再利用EXCEL、LINGO或其他数学应用软件进行求解。求出后，根据市场上的实际价格与要素的影子价格的差异来调整企业的生产资源配置计划。
生产资源规划案例分析
3.1模型建立
一饮料加工厂生产A1、A2两种饮料时采用相同的果汁，设备甲生产3千克A1饮料需要用12个小时并耗费1单位果汁，设备乙用相同原料生产4千克A1饮料需要用8小时，假设生产的商品全都能在市场售出，并且每千克A1获利24元，每千克A2获利16元。现在已知，该加工厂正式工人一天能够劳动的总时间为480小时，供应商每天可以提供50桶果汁进行生产，在设备方面，甲设备每天最大加工量为100kg A1,而乙设备的生产能力没有限制。
现根据上述题目中的约束和信息，请给出下列问题的答案和列出在此条件下企业利益最大的生产计划
1）如果可以用35元的价格买到1桶果汁，是否合算？
2）为适应市场需求，公司时薪将做出调整，临时工的单位工钱最多为多少？
3）通过市场及企业内部信息反应，每生产A1千克的获得的利润将达到30元，现今生产计划是否改变？
该题数学模型：
设每天用x1桶果汁可生产出A1 ，用x2桶果汁可生产出A2
目标函数：
假设每日工厂获利为z元。 x1桶果汁可生产3x1千克A1，获利24*3x1，x2桶果汁可生产4*x2千克A2，获利16*4x2，故z=72x1+64x2
约束条件：
供应约束：已知供应商每天最多能供应50桶用于生产A1、A2，即
x1+x2≤50
时间约束；用于生产A1、A2每天正式工人总的劳动时间不超过480小时即
12x1+8x2≤480
能力约束：设备甲如果全力生产A1每天的加工能力不超过100小时，即
3x1≤100
非负约束：x1、x2均不能为负值，即x1≥0，x2≥0
综上所述可得
max z=72x1+64x2
s.t.
x1+x2≤50
12x1+8x2≤480
3x1≤100
x1≥0，x2≥0
从题目和所建模型中，我们不难看出这是一个线性规划问题，我们要对其求出对应的影子价格，从而给出净利润最大的生产计划。而因为其求解数据可能会收到参数对最优解的影响，所以我们对该模型还需要进行灵敏度分析。
3.2 LINGO求解线性规划
在LINGO模型窗口输入如下：
max=72*x1+64*x2;
x1+x2<=50;
12*x1+8*x2<=480;
3*x1<=100;
单击求解命令（Solve），结果窗口显示如下：
LP OPTIMUM FOUND AT STEP 2
OBJECTIVE FUNCTION VALUE
1) 3360.000
VARIABLE VALUE REDUCED COST
X1 20.000000 0.000000
X2 30.000000 0.000000
ROW SLACK OR SURPLUS DUAL PRICES
2) 0.000000 48.000000
3) 0.000000 2.000000
4) 40.000000 0.000000
NO. ITERATIONS= 2
计算结果表明：在该题线性规划的求解中，用单纯形法进行了两次迭代。最后求出的影子价格为：原料的影子价格：48；工人工时的影子价格为2
为测验该影子价格是否会收到相关参数影响，特进行灵敏度分析测验。灵敏度分析，则LINGO还会输出以下结果：
RANGES IN WHICH THE BASIS IS UNCHANGED:
OBJCOEFFICIENTRANGES
VARIABLE CURRENT ALLOWABLE ALLOWABLE
COEF INCREASE DECREASE
X1 72.000000 24.000000 8.000000
X2 64.000000 8.000000 16.000000
RIGHTHANDSIDERANGES
ROW CURRENT ALLOWABLE ALLOWABLE
RHS INCREASE DECREASE
2 50.000000 10.000000 6.666667
3 480.000000 53.333332 80.000000
4 100.000000 INFINITY 40.000000
计算结果表明，线性规划求解中给出的约束的影子价格仍然是有效的。
综合以上，用LINGO对加工饮料的生产计划分析求解结果如下：
在此案例的约束条件下，企业每天用20桶果汁生产A1类饮料，用30桶果汁生产A2饮料，此计划下一日利润可达最高：3360元；原料的影子价格：48；工人工时的影子价格为2
1）如果可以用35元的价格买到1桶果汁，是否合算？
原料的影子价格为48，由于35 <48, 合算
2）为适应市场需求，公司时薪将做出调整，临时工的单位工钱最多为多少？
工时的影子价格为2，所以工资调整工薪后，临时工的单位工钱最多为多少每小时2元。
3）根据相关信息反应，A1每千克的获得的利润将达到30元，现今生产计划是否改变？
X1原来的系数为243=72，如今利润达到30元后，X1的系数变为30*3=90，均在[64，96] 变化范围内，所以不用更改原计划。
三、总结：
影子价格的应用是运筹学在企业在现实生产生活中的一项重要应用，企业各部门之间形成的各约束条件来建立相应线性规划模型，通过相应软件平台对生产生活中的线性规划中的影子价格进行求解，既可以为企业在生产资源管理和决策分析中提供了重要的依据，又大大降低了不必要的损耗，对提高资源整体利用价值，获得更大经济收益具有更大的现实意义。
参考文献
[1]李林杰,顾六宝，企业经济分析概论[M].中国市场出版社,2004.
[2]徐玖平,胡知能,王矮，运筹学[M].科学出版社,2004.
[3]李慧，资源影子价格分析与经营管理决策[J].系统工程理论与实践,2003,4.
[4]孟红玲，应用数学[M],大象出版社.2007
客服QQ：30444492琼网文【2021】1550-113号
增值电信业务经营许可证：琼B2-20210322
出版物经营许可证：新出发龙华出字第(2021)009号
广播电视节目制作经营许可证：(琼)字第00779号
版权所有 ©2002-2024 期刊网(www.qikanchina.com) 琼ICP备2021005105号
