模糊综合评价法建立10kV电缆故障风险评估体系

模糊综合评价法建立 10kV电缆故障风险评估体系

刘娟

国网南平供电公司 福建南平 353000

引言

随着社会不断发展，电网设备也在快速更新换代。特高压工程逐个建成落地，配网设备逐步支持远程操作，输电导线也从最初的架空线路，逐步演变成了敷设在地下的10kV电缆。架空线路价格低廉，架设方便，适用于远距离输送高压电能。相比于架空线路而言，10kV电缆不容易受外界因素影响，稳定性高，线损量小，更加适合现代城市配电网络建设需求。

同时，为了配合社会的高速发展，对电网的稳定性要求也越来越高。特别就城区而言，停电所造成的影响越来越大，经济损失也越来越难以承受。就国家层面而言，保障居民生产用电已经上升到了国家战略地位。作为配电网络的重要组成部分，10kV电缆运行的安全性与稳定轻有的至关重要的地位。国家电网公司也在一直致力于减小10kV电缆故障率，然而一直无法彻底根除。

就本公司近三年以来的停电故障里，23起故障中共有12起是10kV电缆故障造成的停电，占到了全部停电故障的52.17%，也就是说超过一半的停电故障都是因为10kV电缆故障造成的。电缆因其深埋于地下，日常巡检很难对其运行状态进行准确评估，若要停电进行完整试验检测则将会造成居民频繁停电，实际操作中无法实现。而10kV电缆故障造成的停电影响范围大，抢修难度大，故障查找困难，亟待得到解决。

然而一直以来，对10kV电缆故障的研究一直停留在故障查找的层面，并未对10kV电缆故障风险评估进行过相应研究，所以，本文将使用基于层次分析法的模糊综合评价法，结合最大隶属度原则，通过对近三年10kV电缆故障事件的分析，来进行10kV电缆故障风险评估。

风险评价

10kV电缆故障的风险因素是具体事件，很难用具体数字量化来直接表示，所以这里选择用模糊综合评价法来进行风险评价。

为了建立一套针对10kV电缆故障风险进行科学、有效的评估、判断体系。首先建立一套反映10kV电缆故障风险的定性与定量相结合的二级指标体系。然后采用层次分析法确定各级指标的权重。最后通过对具体10kV电缆所对应的各级风险因素指标进行评价，采用模糊算法计算得到该10kV电缆故障的风险水平。

1.10kV电缆故障风险评价指标体系的设立

于不同的风险因素之间的重要程度存在差异，因此需要对每个因素的权重进行计算

建立层次结构模型

表5 层次结构模型权重设置

判断矩阵如下：

1. 电缆故障风险评价

一致性比例：0.0000;

对"电缆故障风险评价"的权重：1.0000;

λmax：2.0000

2. 电缆本体

一致性比例：0.0000;

对"电缆故障风险评价"的权重：0.6667;

λmax：3.0000

3. 电缆头

一致性比例：0.0000;

对"电缆故障风险评价"的权重：0.3333;

λmax：2.0000

运用层次分析法进行评价，得出各层次的权重，并对结果进行一致性检验。权重向量如下

整体模糊综合评价

得到层次分析法得出的各层次权重之后，我们通过专家评分来判断示例10kV电缆的风险水平。

因为10kV电缆的状态评价受到多种外界因素影响，而专家对于粗略的三个等级评价会受主观影响有较大的误差，不同的专家会对同一个电缆表现有截然不同的程度评价，于是我们采用百分值让专家进行评分。

模糊综合评价是对受多种因素影响的事物做出全面评级的一种十分有效的多因素决策方法，其特点是评价结果不是绝对的肯定或否定，而是以一个模糊集合来表示。

进行模糊综合评价时，目前大多采用专家投票法对隶属度进行确定，这种方法很难保证每个专家对每一个评价对象进行客观可靠的评价，很容易导致隶属度向量趋于均化，我们考虑使用隶属度函数来解决这一问题。

隶属度函数是模糊控制的应用基础，正确构造隶属度函数是能否用好模糊控制的关键之一。隶属度函数的确定过程，本质上说应该是客观的，但每个人对于同一个模糊概念的认识理解又有差异，因此，隶属度函数的确定又带有主观性。

隶属度函数的确立目前还没有一套成熟有效的方法，大多数系统的确立方法还停留在实验和经验的基础上。对于一个模糊概念，不同的人会建立不完全相同的隶属度函数，尽管形式不完全相同，只要能反映统一模糊概念，在解决和处理实际模糊信息的问题中仍然殊途同归。

带入数据后得到

即：

图5 正弦隶属度函数

得出各评价矩阵R_i，如下：

评价矩阵：

评价矩阵：

根据公式得出模糊判断分析集。

判断分析集：

得到总评价矩阵：

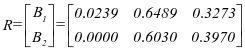
得到总评价模糊判断分析集：

根据模糊分析法中的最大隶属度原则，该电缆属于一般。

有效性检验

对结果的有效性进行检验，最大隶属度原则有效度 指标可以说明采取该原则进行判断时的相对置信度，为评价的结果的合理性提供了定量化描述。即：

其中， 指标等级标准如表2.1所示。

表11 风险评价有效度

综上可得，根据综合模糊评价分析，示例电缆评价等级为一般，不算高风险电缆。

参考文献

[1]陆小义.我国电缆料行业现状与发展趋势[J].扬子石油化工,2006,2(6):48-49.

[2]王少华,叶自强,梅冰笑,等.电力电缆故障原因及检测方法研究[J].电工电气,2011,5:48-51.

[3]罗俊华,邱毓昌,杨黎明.10kV及以上电力电缆运行故障统计分析[J].高电压技术,2003,29(6):14-16.

[4]陈秋,孙正凯,王伟.10kV配网电缆故障分析及防范措施[J].重庆电力高等专科学校学报,2011,16(6):76-78.

[5]董大旻.建设施工危险源研究与管理[M].中国劳动社会保障:北京,2008:65.

[6]谢季坚,刘承平.模糊数学方法及其应用第4版[M].华中科技大学出版社:武汉,2013:95.

[7]郭东星,何大卫.最大隶属原则的有效度在模糊综合评价中的作用[N].山西医科大学学报,1998-02(015).

[8]赵伟舟,王惠珍,张辉,等.基于最大隶属原则和权重策略的自主学习能力评价系统设计[J].计算机与数字工程,2015,11:1981-1984.