基于引力模型的长三角地区航空物流联系程度分析

基于引力模型的长三角地区航空物流联系程度分析

宋舜钰 肖恢翚 顾颖婕 吴沂 顾益菲 周彦雯

上海工程技术大学、上海市 201620

摘要：随着物流产业的蓬勃发展，对我国航空货运运输的质量要求也不断提升，我国航空货运市场高速发展的同时也仍然存在许多问题。本文基于引力模型，选取上海、南京、杭州、合肥、宁波五大城市，构建长三角地区航空物流网络空间结构，计算分析综合物流质量系数，确定长三角地区网络各节点的地位与作用，减少其空间性差异，进而强化区域城市间的合作，以满足区域城市间日益增长的物流需求。

关键词：引力模型、城市物流网络结构、综合物流服务能力

1 引言

在全球经济一体化发展的浪潮下，我国的航空运输产业结构正在发生巨大变化。电子商务的兴起大大增加了航空快件在航空货物中的比例，各大国内枢纽机场均建有航空货运中心，中国航空货运市场也保持着快速增长，为整个航空货运业带来了快速发展的机遇。

2 研究对象与方法

2.1研究对象

长三角地区作为我国的重点经济发展区域，对其航线网络空间结构的分析能进一步了解该区域的航空物流一体化发展状况。拟以长三角地区的航空物流网络为研究对象，利用现有航空交通资源，结合引力模型^[1]及社会网络分析方法^[2]，对长三角地区的各大主要机场所形成的物流网络空间结构进行描述与测度，揭示物流空间联系格局与联系方向。

2.2研究方法

基于引力模型，将模型内的变量内涵重新定义，构建长三角地区间物流空间联系的基础模型如下： 。其中 表示两个节点之间的物流联系， 和 代表每个物流节点的“质量”， 代表两个节点的空间距离， 的值为1。^[3]

3 基于引力模型的城市物流联系值矩阵分析

3.1 数据收集

本文共收集上海、绍兴、嘉兴、南京、扬州、舟山、湖州、南通、泰州、杭州、常州、镇江、合肥、宁波14座城市指标来评定长三角地区各城市的综合物流服务能力，最终选择上海、南京、杭州、合肥、宁波五座城市的各项指标数据均来自于2019年度《中国统计年鉴》以及2019年各市统计局的年度发展公报。

3.2 长三角地区代表性城市的数据分析

根据所收集筛选的数据进行物流联系值计算后，将结果小于1，处于1~10之间，以及大于10的两城市的引力分别定义为弱引力、中等引力以及强引力范畴。

表3.2.1 解释的总方差（主成分贡献率表格）

3.3 SPSS软件—主成份分析法

本文通过使用SPSS软件采用主成分分析法计算长三角地区五座城市的综合物流质量系数，数值越大说明其综合物流服务能力越强。主成分分析法是一种降维统计分析法，可将原来的多个变量化为少数综合统计指标。为了消除不同数量级、量纲带来的影响，需对原始数据进行标准化处理。接着求出各主成分相应的特征值与总和的比例，即为该主成分的贡献率，并降序排列，求得个主成分的累计贡献率。根据计算所得的特征值和累积贡献率分析，可以看到前两个特征值的累计贡献率达到92.024%，说明前两个成分能够描述长三角航空物流网络节点的物流质量系数。具体贡献率表3.2.2所示在得到的主成分分析结果中提取出因子载荷矩阵，即成份矩阵表3.3.1所示。

表3.3.1 因子载荷矩阵（成份矩阵）

将其列入原始数据的表格中，分别命名为a1，a2。提取表3.3中的前两个主成分的特征值，命名为 ， 。接着使用上述两类变量计算标准化特征向量，得到的数值命名为t1，t2，具体计算公式为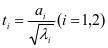 计算主成分得分：

F1=0.33X+0.11X+0.22X+0.21X+0.3X+0.32X+0.33X+0.33X+0.21X+0.33X+0.33X+0.33X;

F2=0.02X+0.62X-0.02X-0.53X-0.24X-0.09X+0.07X+-0.12X-0.48X+0.01X+0.01X+0.08X;

为对长三角区域城市物流质量有一个直观的评价，使用下列计算公式得到其总得分： ，得到综合得分表3.3.2：

表3.3.2综合得分表

4 结果分析

按得分系数排名顺序分别是上海，南京，杭州，宁波，合肥。

由于获得的数据包含负数，因此将“质量”因子的总分线性平移三个单位，再扩大至原来的一百倍，将表3.1.1和表3.1.2中数据和表3.3.3的下半部分数据代入上文的引力模型公式中从而获得长三角各城市之间的物流联系值。

表3.3.3 长三角地区任意两城市的空间距离和物流联系值

5 结论

结果显示出长三角地区节点城市间的航空物流联系程度处于中等水平，但密度标准差较大说明其两极分化的情况较严重；核心区域城市与边缘区域城市的联系较差，呈现出明显的核心边缘结构，这样的网络存在一定的脆弱性，一旦核心节点出现了故障，就会导致整体网络的流通速度降低或者连通性的破坏。

参考文献：

1. 鲁渤、汪寿阳、匡海波.基于引力模型的区域物流需求预测研究，管理评论，2017年02期.

2. 黄维，陈勇.中国教育经济学研究者合作网络的社会网络分析.现代大学教育，2010.

[3]付江月.城市物流网络空间结构集聚与扩散的模型和算法研究[D]. 成都：西南交通大学，2016.