“椭圆及其标准方程”教学设计

“椭圆及其标准方程”教学设计

王芳

新疆伊宁市第一中学 新疆 伊宁 835000

教学目标：

(1)体会画椭圆的过程，并结合自己画椭圆的经历归纳椭圆的定义

(2)理解椭圆的定义，掌握椭圆的标准方程及其推导过程

(3)通过主动探究、合作学习，感受探索的乐趣与成功的喜悦；培养学生认真参与、积极交流的主体意识和乐于探索创新的科学精神

教学重难点：

重点：椭圆的定义及标准方程

难点：椭圆标准方程的推导过程

教学过程：

引入：（PPT展示电影《流浪地球》海报）同学们，前一段时间有一部电影特别火，大家看过吗？跟据学生情况灵活应对，播放电影中的一个片段。

看过这部电影的同学都知道，影片的结局是—地球成功脱离了太阳系，地球在脱离太阳系之前绕太阳公转的轨迹是—椭圆，同学们以前有没有深入研究过椭圆—没有，那今天这节课我们就来研究椭圆及其标准方程。

数学实验：

想一想：

取一条定长的细绳，把它的两端都固定在图板的同一处，套上铅笔，拉紧绳子，移动笔尖，这时笔尖画出的轨迹是一个什么图形？[圆]

画 一画：

如果把细绳的两端拉开一段距离，分别固定在图板的两点处，套上铅笔，拉紧绳子，移动笔尖，这时笔尖画出的轨迹是一个什么图形？

[学生可能会画出椭圆或线段.学生画完图形后进行展示]

教师设问:

（1）在这一过程中，移动的笔尖（动点）满足什么几何条件？

[ 预设：到两定点 的距离的和是常数的点的轨迹是椭圆（教师板书）]

学生想不出来时教师适当引导

比如，将笔尖放在椭圆上的一点处问学生，此时笔尖（动点）到两定点的距离之和是什么？[绳长]再换两个位置让学生回答上述问题

2. 你能结合画椭圆的过程及我们刚才的分析给出椭圆的定义吗？

[到两定点间的距离的和等于常数的点的轨迹是椭圆]教师根据学生的表述板书.

（3）教师演示当绳子绷直时，同学们还能画出椭圆吗？（若有学生在画图过程中考虑到了绳子绷直的情况更好，让学生分析）

[不能，是线段]

（4）说明我们刚给椭圆下的定义还需补充什么条件？

[预设：常数>两定点间的距离]

为了表述方便我们可以用 表示两定点,于是我们可以将上述条件写成常数>

5. 教师找一个不在图板上，但满足到两定点的距离的和等于绳长的点问：

同学们，老师的笔尖现在所在的位置满足到两定点的距离的和等于常数吗？

[ 预设：满足]

教师追问：这个动点的轨迹是什么？ [椭球]

说明我们给椭圆下的定义还需补充 “在平面内”，由此，我们得到了椭圆的定义.

同学们初中时就学习了圆的定义，进入高中后，为了更深入地研究圆，我们研究了圆的方程.类比圆的研究方法，我们研究完椭圆的定义，紧接着来研究椭圆的方程。

上节课我们已经学了求曲线方程的基本步骤：1、建系设点2、写出点集3、列出方程4、化简方程5、检验

接下来我们按以上步骤尝试来求椭圆的方程

教师设问：（1）如何建立合适的平面直角坐标系？

[ 预设：学生可能会有各种不同的建系方法，教师引导学生选择最合理的平面直角坐标系？以 所在的直线为x轴，以线段 的中垂线为y轴]之所以选择这样建系，一方面可以让 的坐标简单一些，另一方面 和 关于原点对称，在化简过程中可能会出现某些项相抵消。

解：设M(x, y)是椭圆上任意一点，椭圆的焦距2c(c>0)，则 的坐标分别是(-c,0)、(c,0) .又设M与 和 的距离的和等于正常数2a (2a>2c) .

由椭圆的定义得：

[引导学生化简方程，可以先让学生思考该如何化简，再带上学生一起化简，化简对学生来说是本节课的难点，若让学生独立完成难度太大，所以教师在引导过程中要注意方法的渗透]

先尝试两边同时平方：

发现运算量很大，有其他方法吗？

可 以将左边的一个根式移到右边，再将这个方程两边平方，发现方程中只含一个根号，将根式放在等式一边，不含根号的项放在等式的另一边，再给方程两边同时平方，整理得 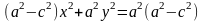_，由于 两边同除以 ，得_，请同学们在右图中找出表示 的线段[学生可能会想到做辅助线]发现_，我们令 ，于是方程可以写成 ①

此时，发现方程的形式更简洁，更对称，我们把方程①叫做焦点在x轴上椭圆的标准方程，两个焦点分别是 ，这里

同理，可以得到焦点在y轴上的椭圆的标准方程[推导过程由学生课下完成，一方面巩固上课所学的方法，另一方面在推导过程中体会焦点在x轴上和焦点在y轴上的椭圆标准方程的内在联系]

知识归纳：

由学生归纳，教师视情况补充

例题精讲：

例1：如果椭圆 上一点P到焦点 的距离等于6

1. 点P到另一个焦点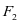 的距离是 14

2. 两焦点坐标分别为 （-8，0） 和 （8，0）

[让学生进一步理解椭圆的定义，能从椭圆的标准方程中找出a,b,并能求出c,能根据椭圆的标准方程判断出焦点所在位置，写出焦点坐标]

例2：写出适合下列条件的椭圆标准方程：

(1)a=4,b=1,焦点在x轴上

(2)a=5,b=3,焦点在y轴上

(3)a=8,b=4.焦点在坐标轴上

答案：（1） ；（2） ；（3）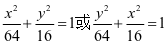

[让学生进一步熟悉椭圆的标准方程，体会在求椭圆标准方程时要注意先确定焦点的位置.渗透分类讨论的思想]

小结：

一、知识层面

（1）椭圆的定义（2）椭圆的标准方程

二、思想方法层面[学生自己总结]