山东省齐河县大黄乡教育学区办公室（ 251103）
在新课标七年级上册数学《同步基础训练》中，有这样一道数学题：
学校建花坛时，留下24米长的小围栏，初一（8）班同学欲利用这些围栏，在自己教室前的空地上，一面靠墙，建一个长方形小花圃。（1）如果小花圃的长比宽多3米，算一算这时的面积；（2）通过改变长与宽，设法扩大花圃的面积，并和其他同学比一比，看看谁设计的花圃面积较大。
这道题第一问的答案在此不必讨论，第二问的答案在《同步基础训练》上如此描述，如图所示：
设花圃长为X,设计最大面积S=X·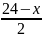
=
=
故 当X=12时，SMAX= 
=72米²
从上述解题过程不难看出，此题运用了初三阶段二次函数求最大值的知识。这对于刚入学不到半年的初一学生来说，远远超出了所掌握的知识范围。若我们用这种方法讲解，同学们无论如何也听不懂，更不用说掌握了。
那么，如何用初一现有的知识来解决此问题呢？下面笔者就谈一谈自己的讲解思路，以供抛砖引玉。
让学生理解题意，可先教同学们看一组例子。
同学们通过观察思考上述例子，可知：两个正因数相乘，一个因数越来越大，另一个因数越来越小，只有两个因数相等时积最大。
有了上述规律，可让学生观察S=X· =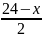
的特点是右边分子是两正数积的形式，分母为定值2，只有当分子（两数的积）最大时，S就最大。再让同学们根据题意想一想，X能否取值1、2、3、4。如果行，再让同学们把x=1、2、3、4带入 S= 可得：
S=
= 
S=
= 
S=
= 
S=
= 
同学们通过观察上式，很快知道，右边分子是两正数之积，且一个因数越来越大，另一个因数越来越小。那么什么时候分子最大，同学们自然猜想出，当一个因数与另一个因数相等时分子最大，也很容易想象出在S= 等式中，当x与（24-x）相等时，分子x（24-x）最大，即S最大。故当X=12时，S最大为72平方米，这样问题就解决了。
由此看来，根据例子找规律，再根据规律做题，所用知识正是初一新生所学知识，适应了循序渐进的思维路径，这完全符合新课标的思想。
【作者简介】李华章（1963.04-），男，汉族，大专学历，山东省德州市齐河县大黄实验小学教师，主要研究方向：数学教育。
客服QQ：30444492琼网文【2021】1550-113号
增值电信业务经营许可证：琼B2-20210322
出版物经营许可证：新出发龙华出字第(2021)009号
广播电视节目制作经营许可证：(琼)字第00779号
版权所有 ©2002-2024 期刊网 琼ICP备2021005105号
