安徽省马鞍山市特种设备监督检验中心,安徽 马鞍山 243000
摘 要:随着工业制造的迅速发展,对测量精度的要求越来越高。三坐标测量机作为一种精密检测仪器设备为制造业向智能化方向发展提供了良好的条件,为了降低三坐标测量机在实际测量过程中存在的误差,建立快速准确的三坐标测量机相关的误差修正模型,应用BP-PSO研究误差建模方法,本文分析了三坐标测量机的误差的来源及特点,利用PSO对BP神经网络进行优化,将优化后的神经网络用于三坐标测量机的误差补偿,并与单独用神经网络优化进行对比,实验表明,运用BP-PSO对三坐标测量机进行误差补偿后的MAE为0.503um,而通过BP神经网络补偿后的MAE为0.544um,则可证明BP-PSO算法具有显著的效果。
关键词:三坐标测量机;误差;PSO;BP
三坐标测量机的组成结构结构复杂且各个子系统之间存在联系,因此三坐标测量机的精度提高,不仅仅依靠某个结构部件的精密度,同时依赖于各子系统之间的相互合作,相互支持。且三坐标测量机的在测量过程中产生的误差与运动速度变化引起的惯性力和振动相关。本文研究的MC850三坐标测量机的结构由机体、导轨支撑系统、驱动及控制系统、测头系统、测量系统、计算机及软件等组成[1][2]。
三坐标测量机的各个主要误差源及相互关联示意图如图(1)所示,各个误差因素不独立,相互关联。从上图中析可以看出要对坐标测量机误差进行精确修正,必须考虑多误差相互制约的影响。为了提高建模精度,必须采用有效的方法进行数据的降维,以提高最后结构的精度,在降维的同时也会一定程度上的减去误差噪声[3][4]。
2.1 PSO
粒子群优化算法(particle swarm optimization,PSO)是一种模仿自然界生物活动的智能全局搜索算法。粒子群算法由于流程简单容易实现,参数简洁。无需复杂的调整,因此非常适合求解优化问题[5],[6],在现实生活中具有较广的运用,并且已经取得了非常显著的效果粒子群优化算法的基本流程如下图2所示[7]。
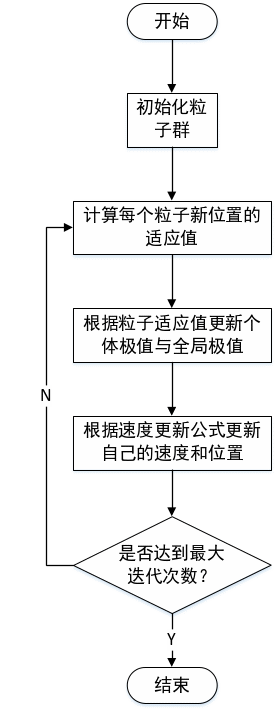
图2 粒子群优化算法流程
2.2 BP神经网络
2.2.1神经网络
将人类大脑中神经元的神经网络的组合复制到人造的模型如下图所示,构建多层神经元,每一层中的神经元都与在其前后层的神经元互相连接。
这样连接一是可以相对容易地编码成计算机指令,二是神经网络的学习过程将会弱化一些实际上不需要的连接,在实际问题中不会产生太大的负面影响[8][9]。
2.2.2 神经网络内部的传递
在神经网络中每个神经元与后一层的连接称为权重,权重的初始值是随机的,随着神经网络的不断学习,权重也在不断地更新。
在隐藏层的每个节点中,我们需要算出组合输入。此处组合是前一层中的原始输出,如下图(4)所示。且这些输出,得到了链接权重的调节。
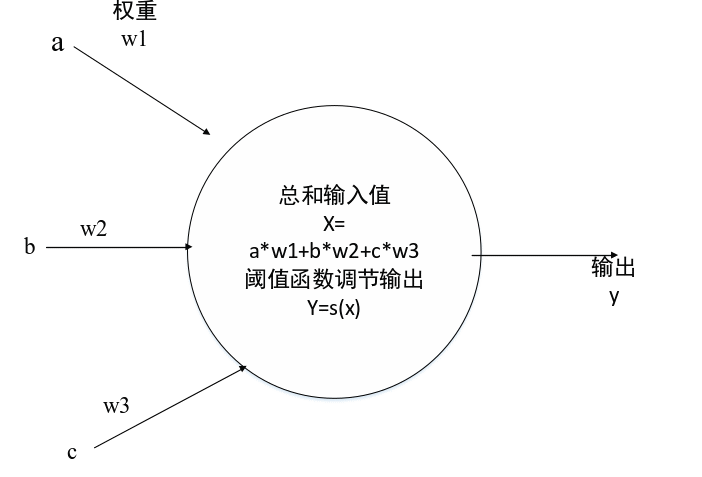
图4 神经网络结点
权重是神经网络学习的内容,这些权重持续优化,得到越来越好的结果。对于前后都是三层的节点,就存在九个权重,输入层为三个节点,根据权重之间的运算,可以得到隐藏层输入的矩阵乘法公式。
X = W*I (1)
在公式(1)中,W为权值矩阵,I为输入矩阵,X为输出矩阵
在神经网络内,我们要将某种称为激活函数的阈值考虑在内,我们一般用S型函数表示神经网络内的激活函数。这个函数相比阶跃函数相对平滑,更接近现实,因为在自然界很少有冰冷尖锐的边缘[10]。
 (2)
(2)
最后一层为输出层,因此假设输入向量为I,则可以都得到隐藏层和输出层的输出如下所示:
 (3)
(3)
由神经网络内部传递机制可得误差传递公式如公式(14)所示。
 (4)
(4)
在BP神经网络中通常将复杂困难的函数当作网络误差,使用梯度下降法对其进行最小化误差。最后通过求偏导得到权值的优化方程,如公式15所示。
 (5)
(5)
则调整后的权值 如下式(16)所示[11][12]。
如下式(16)所示[11][12]。
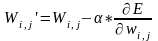 (6)
(6)
3.1交叉验证
为了保证所模型具有很强的泛化能力并且为了应对许多实际应用中数据不充足。可以采用交叉验证的方法。交叉验证的基本思想是重复地使用数据;把给定的数据进行切分,将切分的数据集组合成为训练集与测试集。在此基础上反复地进行训练,测试以及模型的选择。
应用最多的是S折交叉验证。首先随机的将已给数据切分成S个互不相交的大小相同的子集;然后利用S-1个子集的数据进行模型的训练。利用余下的子集测试数据;将这一过程对可能的S种选择进行重复;最后选出S次评测中平均测试误差最小的模型。
3.2实验验证
为了验证本文采用的PSO-BP神经网络的误差修正效果,用三坐标测量机测量一组参数以及已知的准确值作为PSO-BP神经网络的输入值和输出值,并对这组数据进行测试数据和训练数据的划分[13]-[18]。训练样本准备好以后,设定粒子群种群个数s=30,最大迭代次数T=100,定义BP神经网络的参数变化范围,设最大训练次数C的变化范围[100,10000],学习率L的变化范围为[10-1,10-4],利用PSO算法进行参数优化,为再利用神经网络训练的平均绝对误差(MAE)作为评价准则,平均绝对误差越小,拟合效果越好,如表1所示。
算法 | C | L | T | MAE(um) |
BP | 1000 | 0.01 | -- | 0.544 |
BP-PSO | 5000 | 0.023 | 100 | 0.503 |
表1 两种算法在三坐标测量上的均方根误差比较
将两种算法的误差修正值进行比较,由表1可以看出,PSO-BP神经网络的修正值比BP神经网络的修正效果更好。表明了本文所采用算法的有效性。
从两种算法的仿真效果中的适应值变化可以看出,PSO-BP神经网络算法达到的求解精度由于BP算法,根据最后的计算结果显示,通过BP神经网络进行补偿后的MAE为0.544,而通过BP-PSO算法进行补偿后的MAE为0.503,表明PSO-BP神经网络具有更好的补偿效果。
参考文献
陈宁.三坐标测量机测量误差及处理探析[J].仪器仪表标准化与计量,2019(04):42-43.
程湘红. 三坐标测量机测量误差分析及处理[J]. 工程技术研究, 2018, No.17(01):119-120+166.
费业泰, 赵静, 王宏涛,等. 三坐标测量机动态误差研究分析[C]// 全国信息获取与处理学术会议. 2004.
冯同磊. 三坐标测量机动态误差分析与补偿技术研究[D].安徽工业大学,2019.
Fei Chen, Shuhuan Wu, Fang Liu, et al. A Novel Angular-Guided Particle Swarm Optimizer for Many-Objective Optimization Problems. 2020.
张继荣,张天.基于改进粒子群算法的PID控制参数优化[J].计算机工程与设计,2020,41(04):1035-1040.
郝柯羡.基于PSO-SVM的电子商务移动支付风险预测[J].电子设计工程,2020,28(15):79-82+87.
奚之飞,徐安,寇英信,李战武,杨爱武.基于改进粒子群算法辨识Volterra级数的目标机动轨迹预测[J/OL].航空学报:1-25.
吴秀,李晓琴,苏健,孙小莉.基于改进粒子群算法的放射科设备自动化控制方法研究[J].自动化与仪器仪表,2020(07):175-178.
Yang Zhou,Shaojun Li. BP neural network modeling with sensitivity analysis on monotonicity based Spearman coefficient[J]. Chemometrics and Intelligent Laboratory Systems,2020,200.
宋栓军,韩军政,马军.基于BP神经网络的移动机器人避障设计及仿真[J].测控技术,2020,39(04):43-48.
孙艺铭,林雨,范佩升,张丽.基于BP神经网络的智能车电磁导航控制算法[J].科学技术创新,2020(25):103-105.
王光毅.基于BP技术的地质钻探设备工况判别研究[J].自动化与仪器仪表,2020(07):167-170.
王岩雪,孙大跃.基于蚁群算法优化BP神经网络的政务云网络态势预测研究[J/OL].现代电子技术:1-6.
徐佳雄,张明,王阳,程郴.基于BP神经PID的储能电容恒流充电控制系统[J/OL].控制工程:1-5.
郭子奇,杨双锁,李彦斌,杨欢欢,庞星,罗百盛.基于PSO-BP神经网络的地铁盾构场地土体参数反演[J].太原理工大学学报,2020,51(02):171-176.
时维国,雷何芬.基于PSO-BP神经网络的网络时延预测算法[J].自动化与仪表,2020,35(07):1-5.
朱垚锋.基于PSO-BP神经网络盾构掘进参数预测研究[J].建筑机械化,2020,41(06):68-71.