变式教学在中学数学课堂中的应用

变式教学在中学数学课堂中的应用

汪虹佑

重庆文理学院附属中学 重庆市 402160

摘要：变式教学在当今需要改革的课堂上具有非常重大的意义。老师利用变式教学培养学生的思维创造性，提高学生对知识转移过程的了解，培养学生的参与意识，提高学生学习的积极性。通过变式教学可以更好的达到老师为主导、学生为主体的课堂学习模式，让老师的教学变得不再枯燥死板，让学生更有兴趣参与到学习的过程中并享受这一过程。

关键词：变式教学；思维创造性；参与意识；积极性；

从古至今，教育学家一直强调学生应是课堂的主体，老师只是引导学生学习的钥匙。而在教学需要不断变革的今天，怎样让学生更主动的学习成为了众多老师和家长关注的焦点。今天，我们就来浅谈变式教学是怎样提高学生在中学数学课堂上的积极性和效率的。在讨论变式教学的应用之前，我们先来了解变式教学到底是什么。

变式教学中最重要的莫过于变式二字。变式：通过变更对象的非本质特征而形成的表现形式。简单点讲就是变更人们观察事物的角度或方法，从而突出对象的本质特征，突出那些不可见的本质要素。让学生在变式中思维，从而掌握事物的本质和其隐蔽的规律。除此之外，教学二字中的学也是相当重要的，在课堂上老师只是起一个引导者的作用，引导学生进入一道课题，而之后的探究课题就是学生的学了。下面，就让我们来领略变式教学的魅力。

一、利用变式教学，培养思维的创造性

对于老师来说，最成功的教学莫过于让学生的思维主动发散，获得更多的创造性和可塑性。思维的创造性可以让学生跳出题目的误区，从发散思维的侧面读懂题目的本质，探知自身需要的究竟是什么。即变中求进，进中求通，拓展自身发展空间。在这里我们可以采用类比、联想、特殊化和一般化等思想方法进行变式教学。

让我们看看下面这道题：

练习题：

变式一：（2012•南通）已知关于x的多项式 是完全平方式，则常数 等于（ ）

A. 64 B. 48 C. 32 D. 16

变式二：已知关于 的多项式 是完全平方式则 的值为（ ）

A. 2 B. ±2 C. -6 D. ±6

变式三：若关于 的多项式 是完全平方式则 的值是（ ）

A.- 1 B. 7 C. 7或-1 D. 5或1

变式四：已知关于 的多项式 是完全平方式则常数 等于（ ）

以上的练习题和变式题是一种类比式的教学方法，改变了叙述方式和一些变量的取值从而增加题目的难度。这种改变需要学生的发散思维去探索，不能只局限于原练习题。要了解它的更进一层的含义，从而达到思维纵深拓展的要求。

二、利用变式教学进行知识的转移，了解知识的发展过程

在新知识的教学中，注重知识和思维的铺垫，即知识的一环扣一环性。让学生了解知识的发展过程后，也要做好随后而来的知识的转移。让学生利用已有的知识结构来同化新知识，实现知识的迁移。比如：一元二次不等式和分式不等式的承上启下的关系，解分式不等式最重要的解题思想是如何去掉分母。

解下列不等式：

1.     2.     3.  

我们可以通过以上不等式的解决总结解决分式不等式的基本步骤：

1.当分母可以确定正负时，直接去分母；

2.当分母不能确定正负时,通过移项、通分化为 或 形式；

3.转化为不等式 或 ；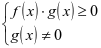

4.解整式不等式或不等式组即可。

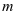巩固提升变式训练：不等式 ，对于任意实数 均成立，求 的范围.

这一组不等式和变式的题既是对新旧知识的融合，也是一个知识发展过程的再现，同时变式训练可补充学生题库的不足性。让学生学习的最佳方法是让学生享受学习知识的过程而不是结果。虽然我们常说一题解，百题解。可是每道题有其不同的特性，也许它在某个方面有着类似性，但变式训练体现更多的是创新。这种创新让学生更了解知识的迁移过程，从而更好的掌握知识、运用知识。

三、利用变式教学培养同学的参与意识，提高积极性

在传统的课堂中，对于一些定理、公理、公式的结论、适用的题型和范围的讲解。老师们总是原原本本的告诉学生，这样不能从根本上激发学生学习的兴趣，只能让学生感到教学的死板性。同时一些同学的听不懂更造成上课玩手机、看小说和打瞌睡等现象的产生。而变式教学就是在老师提出问题后，由同学自己去探究这道题，如何解决的、应用了哪些知识，让学生独立自主回答。这样，一方面提高了课堂的活跃性，加强了师生之间的交流。另一方面，题目梯度性的难度加强激发了学生的挑战心理、调动了学生的积极性、激发了学习的兴趣，让学生更好的融入课堂学习之中。

比如以下关于等比、等差数列的应用：

练习题一：当数列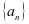 中满足 ， 求数列通项公式.

练习题二：当数列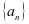 中满足 ， ，求数列通项公式.

变式一：数列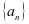 满足 ， ，求通项公式.

变式二：数列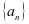 满足 ， ，求通项公式.

以上等差、等比数列的练习题和变式题直观的看，都是用递推公式求通项公式，实则其难度是由易到难的一个阶梯型变化，这种阶梯型的变化是为了培养学生在一点一点的学习累积中的积极性，让学生在不知不觉间获得思维的升华，从而爱上学习的过程。两道练习题可以直接看出是等差、等比数列进而直接带入公式，求通项公式。而变式一、二是启发学生学会等式两边配一个新的常数，进而构造一个新的等比数列，带入公式求通项公式即可。

相信学生们要解决上面的练习题并不是一件困难的事，在此基础上，老师可以提出更深一层的问题。这些问题虽然简单却可以让学生参与其中，从而达到提高积极性的目的。就像著名的教学教育家波利亚说过：”好问题同某种蘑茹有些相像，它们都成堆地生长，找到一个以后，你应当在周围找找，很可能附近就有好几个。”所以变式教学的变可通过改变题目的表达方式，从而为解题增加一定的难度性，而这种难度性恰好可以激发学生的挑战心理，让学生主动去解题即学习。这样，在潜移默化中就培养了学生的参与意识，提高了其学习的积极性。

通过以上对变式教学的了解，我们不难看出。变式教学充分实现了以老师为主导，学生为主体的学习模式。同时变式教学加强了师生之间的交流，让中学生主动去享受学习的乐趣，而不只是被动的接受知识、积累知识，而是自己了解知识的发展过程，自己建构知识体系，为学生自身提供了相互展示、相互学习的机会，营造了一种积极思维，努力上进的学习氛围。变式教学能促进中学生积极主动全面地参与教学全过程，有利于培养学生的创新精神和实践能力。

参考文献：

1. 蓝桂敏.浅谈数学课上的变式教学 .www.pep.com.cn，2011-03-03.

2. 王瑞红，刘锦涛.论高中数学课堂中变式教学的案例分析[J].中学数理化，2014（22）：27-27.