钢结构螺旋楼梯静力非线性分析 2020年 03月

钢结构螺旋楼梯静力非线性分析

王明英 1 丁杭普 2

深圳市建筑设计研究总院有限公司

2.中国五洲工程设计集团有限公司深圳分公司

一．楼梯概况

该楼梯爬行高度5.3米。外环半径2.05米，内环半径0.676米。总旋转度数为540度。楼梯梯段宽1.4米。踏步高处采用[16槽钢。起至端三处采用方通200x150x12(t)。结合建筑造型外环梁采用2根方通440x150x18(t)上下叠加形成，内环梁结合建筑造型要求采用25厚1.1米钢板螺旋成卷。楼梯上下端各设铰支座2个。上支座设置在主体结构梁侧，下支座设置于地面混凝土基础之上。踏步板采用5厚花纹钢板。除踏步板强度为Q235B外其余钢构件强度采用Q345B材料。楼梯抗震等级按三级考虑。该楼梯不同于常规螺旋钢楼梯之处为内环25厚钢板单元，高厚比为1100/25=44。参照《建筑抗震设计规范》GB 50011-2010第8.3.2条工字钢腹板构件宽厚比48相比接近，但该楼梯构件没有翼缘，而且踏步与钢板侧面连接产生面外弯矩。因此该钢板上半段受力为拉弯弯构件，下半段为压弯弯构件。从荷载标准组合弯矩图来开看外环梁截面呈现为全长负弯矩，也即外环梁仅能保证楼梯的整体性，但不能发挥承载力作用。从以上初步分析可知内环钢板构件的截面形态受力环境非常不利。因此有必要对进行专门的分析研究。计算采用SAP2000通用有限元软件。

二．一阶弹性分析

1.由于楼梯体量小自重轻，地震作用不明显故不考虑地震作用。基本荷载组合：1.3D+1.5L。（L=3.5KPA）用于强度计算。标准荷载组合1.0D+1.0L。用于挠度变形计算。

2.内环梁及踏步板采用壳单元建模，外环梁及踏步梁采用杆件单元建模。模型柱网采用圆形柱状轴网，休息平台部位再通过局部修改形成水平面。楼梯上下支座按铰接考虑。模型基本符合建筑尺寸要求。

3.模态信息如下：

其中T1,T2为平动+扭转周期，扭转成分为主。模态工况下的变形揭示T1模态工况下位移最大节点243处U1(全局坐标X向)=279mm, U2(全局坐标Y向)=2mm, U3(全局坐标Z向)=180mm.扭转振型处于主导地位。由于楼梯构件按圆弧方向布置，扭转振动对构件只能产生轴力及弯矩并无扭转的不利影响。T3周期为竖向振动为主，频率f=8.95>3Hz满足规范人行舒适度要求。

4.弹性分析结果：

模型及构件设计验算结果显示构件强度（包括抗剪）应力比不大于0.5。强度设计满足要求。内环钢板梁正应力S11小于345mPa。在弹性变形范围内。正交方向S22及剪应力S12均满足规范强度要求。壳单元应力及杆件应力比见图1、图2。节点编号342为荷载标准组合下最大竖向变形U3=35.3mm。外环钢梁投影长度为C=2*2.05*3.14*（540/360）=19311mm。挠度f=35.3/19311=1/547mm<1>满足要求。构件采用满足经济要求。由于铰接支座对内环梁的弯矩释放，使支座处内环梁（壳）顶出现转角。在工况D+0.5*L下，对该部位进行施工前预调整。分别对内环梁上下支座边缘顶部弧向多预留尺寸9mm，以保证装饰效果达到预期标准。计算变形结果见图3。

图 1

图 2

图
3

5. 一阶段分析小结：

计算结果显示模型指标合理，强度，变形均满足规范要求。但是内环钢板梁局部集中应力已经接近屈服强度。

三．屈曲分析

鉴于楼梯主要支撑构件形态缺陷，采取屈曲分析手段（bucking）验证楼梯整体稳定性。

荷载类型采用1.3D+1.5L。这样的设置方式能直观的看出屈曲因子对于荷载基本组合的放大倍数。输入方式见图4。以模态分析342号节点为监测点。

1.主要屈曲模态因子如下：

以上位移值仅表示屈曲模态下的各阶相对幅度，主要用于判别屈曲形态。屈曲模态第4模态为负值。根据SAP2000技术手册描述，屈曲因子出现负值，表明反向荷载更易失稳，作为楼梯不可能存在反向工况。如果是模态分析出现负特征值表明是结构刚度或质量有问题。对于屈曲分析特征值（屈曲因子）出现负值是正向现象。对于大跨度屋盖出现的负屈曲因子应当引起注意，因为可能的风吸力或活载（雪荷载等）不利布置会导致屋盖失稳。需要多模态的非线性分析。

从屈曲模态表格看到，整体屈曲形态相比于局部屈曲并不明显。也即楼梯整体结构稳定性能良好。第一屈曲模态下，内环梁局部位移幅度突变印证了作者对于该楼梯结构体系初步判断的准确性。参照《空间网格结构技术规程》安全系数K=4.2<6.1，满足安全要求。第一屈曲模态形态见图5。

图 4

图 5

2.屈曲分析小结：

该结构整体稳定性能很高。主要原因是基于楼梯结构不同于普通建筑，楼梯结构具备上下支座的约束，而一般建筑物仅为基础约束，顶部自由。从局部屈曲发生在第一模态可以看出构件的局部稳定需要进入深入分析。

四．非线性静力分析：

结合弹性分析正应力结果及屈曲分析的模态特征。有必要深入的了解该楼梯的工作性能，找出主要构件在塑性状态下的破坏历程。由于该结构分析控制荷载为竖向荷载，因此分析时基于竖向荷载作用下的结构静力非线性分析方法。静力非线性考虑几何非线性及材料非线性。该分析不同于地震作用分析，无法按震级确定性能目标和性能水准。但是可以参照《建筑抗震设计规范》（GB50011-2010）5.5.5条大震弹塑性位移角（1/50）目标位移来进行分析。如果目标位移超过设定限值或结构发生倒塌破坏计算即停止分析。如果各项指标能在规范要求之内。即可判定达到大震不到的性能水准。

构件材料选用如下表：

滞回类型采用Kinematic，随动滞回模型基于在金属材料中普遍存在的随动硬化行为。程序默认将其作为金属材料的滞回模型，该模型耗散的能量可观，适用于延性材料。由于该计算不涉及力的往复，实际上滞回类型不起作用。本构曲线见图6。图中外侧曲线为应变-正应力曲线，内侧曲线为应变-剪应力曲线。

图 6

3.初始缺陷的引入采用目标位移法作为初始缺陷引入点并修改未变形几何。作为非线性分析的激发条件。加载方式采用位移控制，控制节点为342号水平对应内环梁节点341的U1向位移。从楼梯结构形式可以看出内环梁可以简化为两端铰接的简支梁模型。《建筑抗震设计规范》（GB50011-2010）5.5.5条大震弹塑性层间位移角的限值为

[θ_p]=1/50。抗规对应的对象为下部固接，而上部自由。从稳定性及抗倒塌能力来讲要比楼梯的简支梁形式弱。我们知道受压杆件两端铰接状态时的长度计算系数是1,。一端固定一端自由的长度计算系数为2.0。对应以上两种类型，本次分析的层间位移角限值按[θ

_p]=1/25。即U1=2650/25=106mm作为位移目标考虑。实际输入值为110mm。同时对屈曲分析局部变形突出的楼梯上下支座附近节点200-U2,232-U1进行监测。荷载类型同样采用1.3D+1.5L。设定见图7、图8。

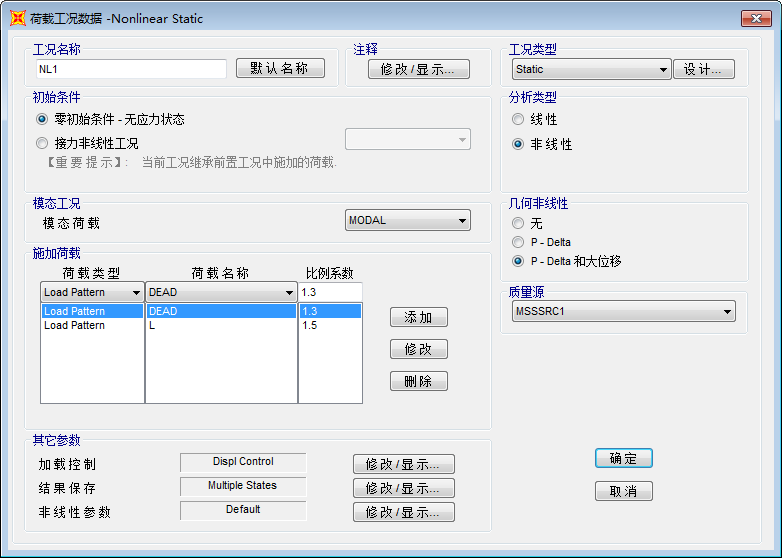
图7

图8

4.分型结果采用绘图函数显示，见图9、图10。横轴为分析步数，竖轴为个检测节点指定方向位移或应力变化。从绘图表格可以看出以指定节点为位移目标下，随着分析步数增加均呈现线性变化，没有突变。节点341在50步位移达到110mm正常收敛，最大正应变值为（E11=-0.0023）,最大剪应力G12（G12=0.0042）均已经进入屈服阶段。有较小塑性变形，属于较轻微破坏。该部位属于正应力，剪应力集中，破坏面积可以忽略不计。

图 9

图 10

5.根据分析图标的线性变化（图11），分析部最大步数50步对应基底反力即为本次计算最大反力，反力值为812KN。D+L工况基底反力为239KN。目标位移下基底反力放大倍数为812/367.69=3.39倍，也即工况（1.3D+1.5L）的2.2倍，工况（D+L）的3.39倍。

6.计算结果图形显示

正应变E11-STEP50,E22-STEP50,剪应变G12-STEP50见图12。节点step-50变形见图13。

图11

图 12

图 13

非线性分析小结：在2.2倍的基本荷载组合作用下，最大侧向位移值等效按简支梁模型考虑挠度为110/5300=1/48，竖向位移挠度为116/19311=1/166。主要构件最大应变局部进入屈服阶段。经过应力平均后最大应力未进入屈服阶段。因此该楼梯变形能力良好。在3.39倍荷载标准组合下达到直立不倒塌。

五．提交主体设计支座内力

支座内力按D+L荷载组合，F3竖向力对主体构件作用按拉负压正方式输入。

总结：

通过一阶弹性分析、屈曲分析、以目标位移的静力弹塑性分析可知该楼梯工作性能如下表：