1.南宁师范大学 数学与统计学院,海南 海口 570100; 2.南宁师范大学 数学与统计学院,广西 南宁 530299
[摘 要]概念、定理是数学知识中的重要组成部分。义务教育2011年数学课程标准中提到:要使学生会探索并证明三角形的内角和定理,掌握它的推论[1]。在数学教学中,学生只有通过自主的思考和操作,才能够建构出相应的知识框架。本文运用APOS理论,以三角形内角和定理的学习为例,使学生从最初剪切、拼接图形层面上升为发现证明三角形定理抽象层面。
[关键词] 三角形内角和定理;APOS理论
[作者简介]张成艳(1996-),女(汉族),海南海口人,南宁师范大学数学与统计学院2019级硕士研究生,主要研究方向为学科教学(数学);韦 宏(1968-),男(汉族),广西上林人,理学硕士,南宁师范大学数学与统计学院副教授,硕士生导师,主要研究方向为学科教学(数学)。
一、APOS理论简述
美国著名教育家杜宾斯基在建构主义学习理论的基础上提出了APOS理论。APOS理论的重点是教师在教学中引导学生通过自己的动手实践,可以学习到相应的数学知识点,还可以分析出相应的数学问题的情境。教师通过学生自主的探索相关的数学知识点,建构出属于自己的数学知识和数学思想方法。杜宾斯基认为:数学教育理论应该致力于“学生是如何学习的”以及“什么样的教学计划可以帮助这种学习的理解”。[2]APOS理论认为:学生通过解决数学问题的过程可以获得相关的数学知识,通过这个过程,学生就可以建立出心理活动、过程和对象,最终建构出用来理解问题情境的图式结构。
二、APOS四阶段
操作阶段,这个阶段是学生能够理解三角形内角和定理的一个重要条件,学生通过操作活动,能够亲自体验、感知问题的直观背景。从而学生能够理解三角形内角和的定理的意义。过程阶段,是学生通过对自己的操作进行思考,可以使学生经历知识内化的过程,学生在头脑中,对自己的操作进行反思,抽象出三角形内角和定理。对象阶段,是通过前面的抽象,初步认识了三角形内角和定理,并且对该定理赋予形式化的定义以及用数学语言进行描述,从而可以达到精致化的程度,使它成为一个具体对象,并且在以后的学习中,学生可以以此为对象去解决新的数学问题。图式阶段,学生需要经过长期的学习活动来逐步完善。学生能够理解三角形内角和定理的意义以及相应的符号表示。能够和其他概念、规则、图形等建立起相关的联系,在头脑中形成综合的图式。
三、基于APOS理论三角形的内角教学过程的设计
(一)第一阶段:操作阶段
引导学生自己动手探索三角形内角和的数量关系,形成对三角形内角和定理的初步认识。通过推理、论证三角形内角和定理,从而使学生掌握它的推论,帮助学生理解三角形内角和定理,有助于后面的学习做好铺垫。
1、探究三角形的内角和
老师:同学们,请你们拿出一张纸,在纸上画出一个三角形,并用标号在所画的三角形上标出三角形的三个内角。标好后,请同学们动手把一个三角形的两个角剪下来,并且拼接在第三个角的顶点处。
教师活动:教师观察全班学生的操作情况
老师:现在大家都已经将三角形其中的两个内角与第三个角拼接在一起,现在请同学们用量角器,动手量量所拼接成的角的度数,你们会得到什么结果?在图二中直线CM与AB是什么关系?在图三中直线MN与BC的关系是什么?你能从中找到三角形内角和的证明方法吗?
设计意图:在APOS 理论的“操作阶段”中,教师通过让学生自己动手操作、观察具体阶段,让学生对三角形内角和定理的形成过程有一个充分体验。通过剪切和拼接的活动,让学生体验动手操作的乐趣,通过教师的引导,学生能够在亲自动手操作的过程中发现证明三角形内和定理的方法。
(二)第二阶段:过程阶段
2、证明三角形内角和定理
教师:请大家思考一下三角形三个内角有什么样的数量关系?请同学们以小组的形式进行讨论,并且证明你们的猜想。(以下图为例进行证明你们的猜想)
学生讨论后猜想:三角形三个内角的和等于180°。
典型例题:如图,已知 ,求证
,求证 。
。

方法1:过点C作 BC的延长线CE,(图略)
BC的延长线CE,(图略)
则 ,(两直线平行,同位角相等)
,(两直线平行,同位角相等)
 (两直线平行,内错角相等)
(两直线平行,内错角相等)
又∵
∴ (等量代换)
(等量代换)
方法2:在 的外部,以AB为一边BD为另外一边作
的外部,以AB为一边BD为另外一边作 ,延长CB到CE(图略)
,延长CB到CE(图略)
∵
∴ (内错角相等,两直线平行)
(内错角相等,两直线平行)
∴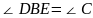 (两直线平行,同位角相等)
(两直线平行,同位角相等)
又∵
 (等量代换)
(等量代换)
方法3:过点A作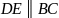 (图略)
(图略)
∵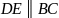
∴ (两直线平行,内错角相等)
(两直线平行,内错角相等)
 (两直线平行,内错角相等)
(两直线平行,内错角相等)
又∵
 (等量代换)
(等量代换)
教师活动:教师引导学生从前面的操作中得到证明三角形内角和定理的方法,并且引导学生规范的写出证明的过程。
设计意图:在APOS理论的“过程阶段”中,学生在教师的引导下,能进行思维的概括并且得出三角形内角和的定理。学生在前面的操作过程中对三角形内角和定理形成了初步的认识,学生通过初步认识的基础上进行小组通过讨论得出猜想,在老师的引导下学生证明三角形内角和等于180°的猜想是正确性,为学生后面能过够更好解决数学问题做下铺垫。
(三)第三阶段:对象阶段
3、三角形内角和定理符号的表示
教师:哪位同学能够运用自己的语言把你们的猜想描述以一下呢?
学生回答,教师用规范的语言重新描述一遍三角形内角和定理
教师:同学们描述的非常好,这就是我们这节课的学习重点内容:三角形内角和定理。
三角形内角和定理:三角形三个内角的和等于180°[3]。
老师:你们会运用几何语言描述三角形内角和的定理吗?
几何语言:在 中,
中,
设计意图:在APOS理论的“对象阶段”中,学生认识到了数学定理的本质,并且能够使它符号化。学生在一定程度上达到了一个精致化的过程。本节课教师通过引导学生进行过程的学习,抽象出三角形内角和定理的文字表达,以及数学符号表示,为后面的学习奠定基础。
(四)第四阶段:图示阶段
4、例题展示
教师利用多媒体展示例题1,例题2,并且要求学生独立完成。
学生说出解题过程,教师讲评,规范书写格式
例题1:如图,在 中,
中, °,
°, °,AD是
°,AD是 的角平分线,求
的角平分线,求 的度数。
的度数。
学生说出解题过程,教师讲评,规范书写格式
解:在 中,
中,
∴
=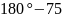 °-
°- °=40°
°=40°
∵ °,AD是
°,AD是 的角平分线
的角平分线
∴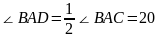 °
°

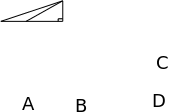
例题2: 如图,从C处观测A、B两处时视角 °从B处观测C处时仰角
°从B处观测C处时仰角 °,从A处观测C处时仰角
°,从A处观测C处时仰角 。
。
解∵
∴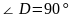
在 中,
中,
∴
=
∴
在 中,
中,
∴ =
=
设计意图:学生对操作阶段、过程阶段、对象阶段的认知结构与三角形内角和定理进行整合,在头脑中产生新的图式,并且这个图式能够判断与这个定理相关联的问题是否属于这个范围。学生通过这个阶段的学习,能够掌握三角形内角和的定理,并且能够熟练的运用这个定理去解决其他数学问题。
四、课堂练习
练习1:如图,在 中,
中, ,BD平分
,BD平分 ,求
,求 的度数。
的度数。

练习2课本13页第2题
五、课后作业
课本16页第1、3、4题
六、课堂反思
1、本节课通过让学生自己动手画出三角形,标出三角形三个内角的编号,剪下三角形其中两个内角,并且通过拼图等活动以及相关的证明,证明出了三角形内角和定理,使学生从剪图和拼图中得到启发,并且学生能够用多种方法证明三角形内角和定理。
2、通过本节课的学习,学生掌握了三角形内角和的定理以及总结出了直角三角形的两个锐角互余。学生通过本节课的学习,学会了应用三角形内角和定理去解决其它的数学问题。
3、布鲁纳认为教学应该是在教师的引导下,学生自己去发现的一个过程。由学生自主探索生成知识,从发现问题到解决问题的过程中,逐渐形成了一定的数学问题意识[4]。
参考文献
[1]中华人民共和国教育部.义务教课程标准[M].北京;北京师范大学出版社,2011.
[2]马力仲.图式理论与中学数学教学[M].四川人民出版社,2015.11.
[3]义务教育教科书数学九年级上册 [M]. 北京 : 人民教育出版社 ,2014.
[4]沈仁广.论中学数学探究学习的价值取向———以勾股定理教学设计的改进为例[J].数学通报,2012(9).