排序问题在林场中的应用

排序问题在林场中的应用

李晓明

甘肃省小陇山林业实验局李子园林场 甘肃天水 741005

摘要：林场管护林地面积广阔，易发多处林区病虫害或者小型火灾，我们无法同时处理问题林区，只能一一处理，然而问题林区的处理时间往往与等待时间有关，等待时间越长，处理时间越长，为了减少损失，我们需要找到所用时间最短或费用最少的方案，这里可以用到组合优化中的排序理论。

关键词：处理时间；等待时间；排序

1引言

在现实中，林区的处理时间往往与等待时间相关，且往往随着等待时间增长，如发生火灾，如果救灾晚的话，可能发生大火蔓延，使救灾时间延长。这类处理时间依赖等待时间的排序问题中，林区的实际处理时间通过基本处理时间，增长率和等待时间来确定。

2问题表述

在这些问题中林区处理时间的增长率可能与基本处理时间相关，如果我们认为林区的等待时间与基本处理时间成正比即 ，则林区的实际处理时间为 ，我们将 称为增长函数或恶化函数，不失一般性，可以将增长函数设为 。

于是，我们可以给出林区处理时间的增长率与基本处理时间相关的问题的描述：设有n个林区 ，林区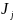 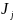的等待时间为t，增长函数为 ，其中a，b均为非负常数， ；构造完工时间 的非减函数 则最大费用 。所以排序问题记为

3算法

3.1问题

问题 中其最大完工时间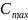 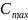与林区处理顺序无关，若第一个处理的林区等待时间为 ，则最大完工时间为：

证明：设在某排序中，林区处理顺序为π=[ ],第一个处理的林区等待时间为 ，则

设对第k个林区 有：

则第k+1个林区 有：

由归纳假设，对第n个林区 有（*）式成立。所以

由于在（*）式中，每个林区的处理时间都是对称的，因此对于林区的任何处理顺序（*）公式均成立。

3.2问题

问题 对于目标函数与工期有关的情况，研究一般性的极小化最大费用问题 ， ，其中 是完工时间 的非减函数。

有上述3.1可知，对于给定的林区集合，最大完工时间与林区处理顺序无关。根据这一性质和 是完工时间 的非减函数，可以构造求解问题 的多项式算法。算法的思路是从后到前确定各林区的处理顺序，使每次确定排最后的林区的函数值都是最小的，从而保证整个排序是最优排序。

算法：设A={尚未确定处理顺序的林区}；B={已经确定处理顺序的林区}

1. 置A={ }；B=∅.

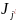
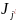2. 对当前时刻的A，记 ，求 ，使

将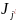 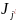排在最后一个位置。置A=A-{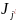 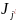}；B=B+{ }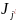

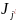3. 若A=∅，停止：否则转步骤（2）。

证明此算法得出的排序是最优排序：

设π为一个最优排序，π中林区的处理顺序与算法给出的排序中林区处理顺序不同，不失一般性，先设最后一个林区不同。

设π为如下形式

其中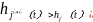 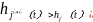， 与 代表剩下的林区。

由于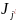 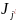也可以排在最后，在π中将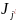 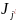取出排在最后一位，得到一个新的排序

从π变成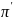 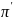的过程中除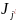 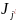外其余林区的处理时间都没有增加，因为 是完工时间 的非减函数，所以这些林区的 不会增加，又因为 所以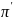 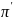的目标函数值不会超过π的目标函数值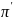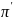， 中的最后一个林区与算法给出的排序的最后一个相同，还是用这种方式将最优排序π继续转化，每一步转化都可以保证产生的新的排序的目标函数值不会增加，直到转化为有此算法产生的排序而且目标函数值不变，所以该算法得出的排序是最优排序。

4结语

这样借助于组合优化的理论，可以得出这一类林业问题的算法。在林场工作实践中会遇到各种各样的问题，要善于总结、归纳、抽象，同时还可以结合其他专业、学科，这样不但可以开拓思维，也便于更好的解决问题。

参考文献

[1]唐恒永，赵传立.排序引论[M].北京，科学出版社，2002年6月第一版.

[2]王吉波.工件加工时间可变的现代排序问题[D].大连，大连理工大学，2005.