上海市金汇实验学校 上海市 201101
闵行区“推进中小学课堂教学改进三年行动计划(2016-2018年)”中提出:“将评价贯穿于教学的过程之中,教师要高度重视课堂观察与评价反馈,要让学生展示思维过程,暴露思维问题并及时反馈矫正。”教师的课堂教学中,应该依据教学内容并针对学情,精心设计与教学目标相匹配、适合学生、难度适宜的课堂习题,及时掌握学生的学习情况进行评价,并及时纠正。笔者在新授“解直角三角形的应用”时,针对例9设计课堂习题,在任教的班级进行了教学,取得了良好的教学效果,具体实施过程如下:
一、案例题目
例 9 如图,小明想测量塔
9 如图,小明想测量塔 的高度.塔在围墙内,小明只能在围墙外测量,这时无法测得观察点到塔的底部的距离,于是小明在
的高度.塔在围墙内,小明只能在围墙外测量,这时无法测得观察点到塔的底部的距离,于是小明在 处仰望塔顶,测得仰角为
处仰望塔顶,测得仰角为 ,再往塔的方向前进
,再往塔的方向前进 米至
米至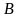 处,测得塔顶的仰角为
处,测得塔顶的仰角为 ,(点
,(点 、
、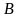 、
、 在一直线上),小明能测得塔的高度吗(小明的身高忽略不计,结果精确到
在一直线上),小明能测得塔的高度吗(小明的身高忽略不计,结果精确到 米)?
米)?
例题分析:本节课的教学目标是引导学生进一步学习解直角三角形知识的应用,解决工件设计中的简单计问题以及测量位置高度差和底部不能达到的物体高度的简单实际问题。本题是测量底部不能到达物体的高度。在教学过程中,引导学生将实际问题抽象为数学问题,运用方程来解决几何计算。
解法:设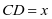 ,
,
在 中,
中,
 ,
, ,
,
在 中,
中,
 ,
, ,
,
 ,
,
 ,
,
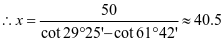 (米)
(米)
答:塔的高度约为40.5米。
二、教学实录片段
习 题1 在
题1 在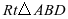 中,
中, ,
, ,
, ,
, ,尝试表示
,尝试表示
解法:设 ,
,
在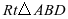 中,
中,
 ,
, ,
,
在 中,
中,
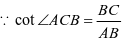 ,
, ,
,
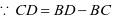 ,
,
 ,
,
 ,即
,即
设计意图:本题为例9出现的数学模型,将实际问题转化为一般图形问题。鼓励学生自主研究,领会方程思想,让学生展示思维过程,及时评价并反馈对例9的掌握程度。
评注:从课堂学生的解答情况来看,学生能够及时掌握解决这个一般形态问题的关键在于:一是对基本图形有充分的认识,二是对解直角三角形的几何计算基本方法;三是利用方程解决几何问题。
习 题2 (1)如图,当α=30°,β=45°,m=2时,AB=________;
题2 (1)如图,当α=30°,β=45°,m=2时,AB=________;
(2)如图,当α=30°,β=60°,m=6时,AB=________;
设计意图:习题1是针对例9的数学模型的总结归纳,找出一般结论,通过习题2的快速代入计算,加深对该结论 的印象,并考察特殊锐角三角比。
的印象,并考察特殊锐角三角比。
评注:从课堂学生的解答情况来看,学生基本能够对该结论有较好的记忆,对此基本图形有一定的印象。
习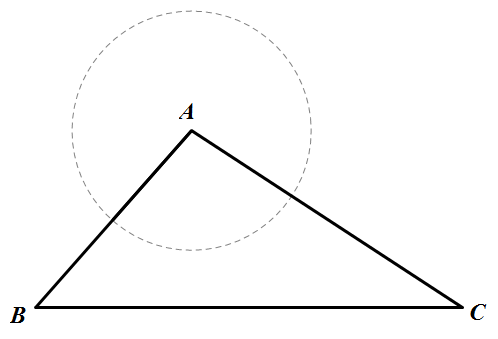 题3 如图,点
题3 如图,点 一个半径为
一个半径为 米的圆形森林公园的中心,在森林公园附近有
米的圆形森林公园的中心,在森林公园附近有 、
、 两个村庄,现要在
两个村庄,现要在 、
、 两村庄之间修一条的笔直公路将两村庄
两村庄之间修一条的笔直公路将两村庄 、
、 连通.经测量
连通.经测量 ,
, ,
, 米,问此公路是否会穿过森林公园?请通过计算进行说明.
米,问此公路是否会穿过森林公园?请通过计算进行说明.
解 法:过点
法:过点 作
作 交
交 于点
于点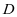
设 米,
米,
在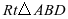 中,
中,
 ,
,
 ,
,
在 中,
中,
 ,
,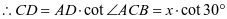 ,
,
 ,
,
 ,
,
 ,
,
所以,公路不会穿过森林公园
设

计意图:习题3主要就是求点A到BC的距离,从两题的数学模型中可以看出,习题3是例9的变式,解法上相同,都是利用方程的思想来解决问题。本习题的一个重要目标是培养学生思维能力,提高学生思维灵活性,在理解原例题的基础上,灵活运用数学思想方法,指导学生领会化归思想、方程思想在几何计算中的运用,从中体会数学思想方法对解决问题的重要意义。
评注:从课堂学生的解答情况来看,学生能够及时掌握解决这个变式题的关键在于:一是对例9基本图形有充分的认识,两个基本图形之间的关系,从图中可以发现习题3中的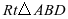 相当于是例题中的
相当于是例题中的 关于
关于 翻折得到的,解题思路基本一致;二是利用方程解决几何问题。
翻折得到的,解题思路基本一致;二是利用方程解决几何问题。
三、教学感悟
本节课笔者基于学情,设计的课堂习题从实际问题转化为一般问题,再由基本图形复杂化。课堂习题引导学生通过感知、概括、应用的思维过程去掌握规律。在课堂教学中,通过课堂习题的逐步推进,将重点问题层层剖析,使学生关注解决问题的本质,再充分利用学生在课堂中生成的资源,将暴露出的思维问题及时评价、纠正,更加有效地提高了课堂教学效果。
作者简介:黄舒文(1991-),女,上海人,本科,毕业于上海师范大学,初级教师,具体的研究方向为初中数学。