将数学史融入相似三角形应用的教学设计

将数学史融入相似三角形应用的教学设计

张成艳 1，韦宏 2

南宁师范大学 数学与统计学院，海南 海口 570100； 2.南宁师范大学 数学与统计学院，广西 南宁 530299

[摘 要]不同数学知识的产生都有其相应的数学文化背景。把数学史融入数学课堂中，可以让学生体会到相关数学知识的形成过程。将数学史融入“相似三角形应用”教学中，不仅可以加强学生对数学知识点理解，而且还可以让学生体验古代数学家创造数学知识的过程，从而进一步提升自身的数学文化素养。

[关键词] 数学史；相似三角形；应用；教学设计

[作者简介] 张成艳（1996-），女（汉族），海南海口人，南宁师范大学数学与统计学院2019级硕士研究生，主要研究方向为学科教学（数学）；韦 宏（1968-），男（汉族），广西上林人，理学硕士，南宁师范大学数学与统计学院副教授，硕士生导师，主要研究方向为学科教学（数学）。

在相似三角形的应用课中，融入数学史进行教学，可以创造历史背景，让学生体验数学知识的“再创造”过程。在数学的发展历程中，每一个数学知识点的产生，都体现出不同的数学文化背景。在教学过程中要重视数学史融入数学课堂教学中，要引导学生了解数学的发展历史，感受数学史在数学中的重要作用。在初中数学课程标准的引领下，教师在教学中要注重数学史走进课堂的教学。数学史走进数学课堂中，不仅能够激发学生学习数学的兴趣，而且还能够丰富教师的教学方法，使教师在数学教学中树立立德树人的根本思想。本篇文章是以九年级下册数学课本中《相似三角形应用》这一课时为例，把数学史融入《相似三角形应用》这一课时内容中进行教学设计分析。

一、教材内容分析

《相似三角形应用举例》这一内容是人教版数学课本九年级下册第二十七章第二小节第三课时的内容，是学生初中数学学习的重要内容之一。运用相似三角形的性质，我们可以解决生活中的一些测量问题。在日常生活中有一些大型的建筑物，我们无法直接的去测量，但是我们可以应用相似三角形的判定方法去构造两个相似三角形，从而去计算大型建筑的高度。运用相似三角形的性质，我们可以去计算不能直接测量的物体高度，可以解决生活中的很多实际问题。让学生在数学学习的过程中感受到数学是来源于生活，同时也是应用于生活的。通过《相似三角形应用举例》的教学，可以为学生几何的推理打下基础，为后面高中的几何学习做好铺垫。

二、学生的学情分析

学生在学习《相似三角形应用举例》这一节内容之前就已知学习了图形的相似、相似三角形的判定及相似三角形的性质。学生对相似图形已经有了一定的了解，同时也初步掌握了如何判定两个三角形相似的方法和两个三角形相似的性质。但是，本阶段学生数学知识的应用能力比较差、数学的应用意识相对比较弱。在数学学习中可能会出现：学过的知识不懂得运用来解决生活中的实际问题。因此，本节课以相似三角形知识点的应用为教学难点，重视引导学生运用所学过相似三角形的有关知识点去解决实际问题，将生活中的实际问题转化为数学问题，运用所学的知识去建立数学模型，从而进一步提高学生应用所学过的知识去解决生活中的问题的能力，加强学生的应用意识。

三、教学目标

《相似三角形应用举例》这节课的教学目标有：1、学生能够进一步加深对相似三角形的判定方法和性质的理解；2、让学生体会如何运用已学过的数学知识来解决实际问题；3、让学生体会运用数学知识解决实际问题的成绩感，感受数学文化。

四、教学方法

《相似三角形应用举例》这一节课运用的是数学历史进行教学的方法（即发生教学方法）和探究式教学方法进行教学。通过对数学问题的探究，向学生展示古代数学家运用相似三角形的判定方法和性质解决生活中问题的情境。将古希腊数学家泰勒斯的测量方法引入到本节课的学习讨论中，不仅有利于激发学生数学学习的兴趣，而且还有利于让学生感受数学知识的“再创造过程”。

五、教学过程

（一）历史问题创设情境，回顾旧知识

问题1：古希腊著名数学家泰勒斯通过运用相似三角形的原理，就测量出了金字塔的高度。前面我们已经学习了相似三角形的判定方法和相似三角形的性质，你们能利用所学过的知识测量出金字塔的高度吗？

师生活动：教师展示埃及金字塔的图片及数学家泰勒斯测量金字塔所构造的图形。（图略）教师引导学生复习相似三角形的判定方法及其相似三角形的性质。学生回顾前面所学过有关相似三角形的知识。

设计意图：以测量埃及金字塔高度的问题来创设问题情境，展示埃及金字塔的图片目的是为了让学生感受当时的数学环境是没有办法直接测量金字塔的高度的，进一步让学生体会到古代数学家的聪明。在探究如何测量金字塔高度前，引导学生复习相似三角形的判定方法及其相似三角形的性质，可以加深学生对旧知识的理解和加强学生运用旧知识的能力。

（二）探究新知识

1、分析特例，融入数学史

问题2：据传说，古希腊数学家、天文学家泰勒斯曾用相似三角形的原理，在金字塔影子的顶部立一根木杆，借助太阳光线构成两个相似三角形，来测量金字塔的高度。如图，木杆EF长2 m，它的影长FD为3 m，测得OA为201 m，求金字塔的高度BO^[1]。

解：∵太阳光是平行光线

∴

又∵

∴

∴

∴ (m)

师：数学家泰勒斯能够测量出金字塔的高度，最主要是运用相似三角形的原理。这一原理的运用其实离不开著名数学家笛沙格的定理（笛沙格定理：两个三角形ABC和A'B'C'的对应点连线AA'、BB'、CC'经过同一点的充要条件是它们的对应边BC和B'C'、CA和C'A'、 AB和A'B'的交点共线）。教师利用多媒体播放证明笛沙格定理的小视频。

设计意图：通过再现泰勒斯测量金字塔的过程，让学生体会在实际测量物体的高度时，关键是要构造实物所在三角形及与实物所在的三角形相似的三角形。而且在构建的三角形中也要能测量出相关线段的长。播放小视频可以吸引学生的注意力，从而可以进一步激发学生数学学习的兴趣。

2、教师向学生展示中国式的相似理论——勾股不失本率（即相似三角形对应边成比例）

问题3：（来自《九章算术》）今有勾五步，股十二步。问勾中几何？（图略）

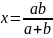数学家刘徽按“勾股不失本率”原理计算如下：小勾股：勾、股之和 ,勾长x；大勾股：勾、股之和 ,勾长a,由“不失本率”原理得： ,即^[2]。

设计意图：向学生展示我国古代数学家刘徽利用勾股不失本率原理测量物体的长度的过程，让学生感受古代数学家的智慧以及遇到的难题。

（三）课堂练习

1、在 某一时刻，测得一根高为1.8 m的竹竿的影长为3 m，同时测得一栋楼的影长为90 m，这栋楼的高度是多少？^[1]

2
、铁道口的栏杆短臂长1m,长臂长16 m,当短臂端点下降0.5m时,长臂端点升高多少米？

设计意图：通过练习，加强学生对相似三角形相关知识点的巩固；加强学生应用数学知识的去解决生活中问题的能力。

（四）课堂小结

1、本节数学课我们学习了什么内容？

2、一个不可以直接测量的物体的高度一般用什么方法解决？

（五）课后练习

1、课本P43,第9、10题

2、请同学们课后网上查找历史上有关相似三角形应用的题，然后小组成员之间进行合作交流、探讨出所找到的题目的解法。

设计意图：通过练习加深学生对相似三角形有关知识点的应用，同时通过小组之间的合作查找有关历史资料和探讨解法，加强学生的合作意识，以及丰富学生的数学史知识，进一步提高学生的数学文化素养。

（六）教学小结

结合教材的内容和学生的学习情况，我将本节课的教学设计进行了四次渗透数学文化。首先是以古希腊数学家泰勒斯的故事导入本节课所学习的内容，激发学生的学习数学兴趣；第二，在探索金字塔的测量方法时，介绍古希腊数学家泰勒斯测量金字塔的过程，播放小视频使整个教学过程变得生动有趣，调动学生学习的积极性；第三，再次展现示古代数学家遇到的难题，展示我国数学家刘徽运用中国式的相似理论解决测量问题的过程。让学生感受数学文化的博大精深和体会古代数学家的智慧；最后，在布置作业时，要求学生去查找有关相似三角形应用的例子。整节课的教学过程注重数学文化的渗透。在数学教学过程中渗透数学文化，可以引发学生对数学问题的思考、调动学生学习的积极性。同时可以加深学生对数学文化的理解，从而进一步提高自身的数学文化素养。

参考文献

[1] 义务教育教科书数学九年级下册 [M]. 北京 : 人民教育出版社 ,2014.

[2]林永伟，叶立军编著.数学史与数学教育[M].杭州：浙江大学出版社.2004.