(云南大学旅游文化学院信息学院 , 丽江 674199)
摘要:本文主要讨论了高阶kirchhoff方程的整体吸引子,对于低阶kirchhoff方程的整体吸引子,已有相当的研究.本文在低阶型kirchhoff方程研究的基础上,研究了一类广义非线性高阶kirchhoff型方程的整体吸引子.首先,在对高阶kirchhoff方程中的非线性项做出合理的假设下,得到方程的整体解和吸收集,然后由整体吸引子的判定定理(渐近紧性),得到此类高阶kirchhoff方程的整体吸引子.
关键词:高阶Kirchhoff方程;整体解;吸收集;整体吸引子
中图分类号:O175
Global Attractor for a Class of Generalized Nonlinear nonlocal Higher-Order Kirchhoff Type Equations
LU Jingxin
(1Department of Information, Tourism and Culture College of Yunnan University,Lijiang,Yunnan 674199
2School of Mathematics and Statistics,Yunnan University,kunming 650500,yunnan,China)
Abstract:In this paper, we mainly discuss the global attractor of higher order Kirchhoff equation. For lower order Kirchhoff equation, the global attractor has been studied considerably. In this paper, the global attractors of a class of generalized nonlinear higher-order Kirchhoff equation are studied on the basis of the study of lower-order Kirchhoff equation. Firstly, under the reasonable assumption of the non-linear term in the higher-order Kirchhoff equation, the global solution and the absorbing set of the equation are obtained. Then, the global attractor of the higher-order Kirchhoff equation is obtained by the determination theorem of the global attractor (asymptotic compactness).
Key words:Higher-Order Kirchhoff equations;global solutions;absorbing set;global attractors
本文研究下列非线性高阶Kirchhoff型方程的整体吸引子:
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
其中![]() 是RN中具有光滑边界的有界域,而有关
是RN中具有光滑边界的有界域,而有关![]() 的假设将在后文中给出.
的假设将在后文中给出.
1883年Kirchhoff在研究弹性横截面运动时,建立了下列方程
![]() ,
,
作为描述该运动模型,其中![]() 是形变静止能量的一部分.此方程比经典波动方程更准确的描述了弹性杆运动.因此后人将此类方程命名为kirchhoff方程.
是形变静止能量的一部分.此方程比经典波动方程更准确的描述了弹性杆运动.因此后人将此类方程命名为kirchhoff方程.
关于低阶kirchhoff方程已有很多深入的研究[1-11],Yang Zhijian[1]也研究了在![]() 中具有强阻尼项的Kirchhoff型方程的长时间行为:
中具有强阻尼项的Kirchhoff型方程的长时间行为:
![]() , (4)
, (4)
其中![]() ,
, ![]() .
. ![]() 是具有光滑边界
是具有光滑边界![]() 的有界域,
的有界域,![]() 是一个外力项。文章证明了有关连续解半群
是一个外力项。文章证明了有关连续解半群![]() 拥有整体吸引子,同时存在有限分形维数和Hausdorff维数.
拥有整体吸引子,同时存在有限分形维数和Hausdorff维数.
Igor Chueshov[2]研究了下列具有非线性强阻尼的Kirchhoff波方程的长时间行为:
![]() , (5)
, (5)
Penghui Lv,Jingxin Lu和Guoguang Lin[3]证明了下列广义非线性Kirchhoff方程的整体吸引子:
![]() , (6)
, (6)
该文得到了半群![]() 在空间
在空间![]() 中存在整体吸引子,同时Penghui Lv,Xiaojun Lv[4]在文献[3]的前提下进一步证明了半群
中存在整体吸引子,同时Penghui Lv,Xiaojun Lv[4]在文献[3]的前提下进一步证明了半群
![]() 存在
存在![]() 整体吸引子.Penghui Lv,Jingxin Lu[5]在文献[3]的基础上证明了下(1.6)的惯性流形吸引子.
整体吸引子.Penghui Lv,Jingxin Lu[5]在文献[3]的基础上证明了下(1.6)的惯性流形吸引子.
整体吸引子是研究具有耗散项的非线性发展方程的渐近性行为的基本概念,关于低阶kirchhoff方程的整体吸引子问题已经有很多深刻的结论,但是关于高阶kirchhoff方程的整体吸引子的研究相对较少[12-14].
最近,Yuting Sun, Yunlong Gao, Guoguang Lin在文献[12]中讨论了下列高阶kirchhoff方程的整体吸引子:
![]() , (7)
, (7)
Yunlong Gao, Yuting Sun, Guoguang Lin[13]研究了下列具有强线性项的高阶非线性kirchhoff方程的整体吸引子:
![]() , (8)
, (8)
同时该文还对Hausdorff 维数和Fractal维数进行了估计.
为方便读者,本文结构如下:在文章第2部分中,给出主要记号和主要整体吸引子的相关理论和结论.第3部分,我们证明了方程整体解得存在性.第4部分,我们证明了方程对应的算子半群![]() 在相空间
在相空间![]() 中存在整体吸引子.
中存在整体吸引子.
为叙述方便,引入下列符号:
![]()
![]() .
.
其中![]() ,
,![]() 为
为![]() 的共轭空间,p´=p/(p-1).
的共轭空间,p´=p/(p-1).![]() 是L2-内积下的Sobolev空间,同时
是L2-内积下的Sobolev空间,同时![]() 表示
表示![]() 在
在![]() 中的闭包(
中的闭包(![]() ),符号
),符号![]() 表示H-内积.
表示H-内积.
定理1 假定:![]() ,正常数
,正常数![]() ,
,
![]()
![]() ,
,![]() ,
,![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ;
;
![]()
![]() ,
,
则问题(1)~(3)存在唯一整体解![]() ,
,![]() .
.
定义映射![]() ,其中
,其中![]() 是问题(1)~(3)的解.根据定理1,
是问题(1)~(3)的解.根据定理1,![]() 构成在
构成在![]() 上的连续算子半群.
上的连续算子半群.
引理1[6] 由![]() 假设成立,则任意的
假设成立,则任意的![]() ,存在
,存在![]() 和
和![]() ,对所有
,对所有![]() ,某些独立于
,某些独立于![]() 的
的![]() ,使得
,使得
![]() , (9)
, (9)
![]() , (10)
, (10)
![]() . (11)
. (11)
定理2 在定理1的条件下,上述连续算子半群![]() 在
在![]() 中存在有界吸收集.
中存在有界吸收集.
定理3 在定理2的条件下,上述连续算子半群![]() 在
在![]() 中存在整体吸引子
中存在整体吸引子![]() .
.
引理2[6] 设![]() 在
在![]() 为非负局部可积函数,且
为非负局部可积函数,且![]() 为绝对连续的,若对于某个
为绝对连续的,若对于某个![]() 和
和![]() 满足下列不等式:
满足下列不等式:
![]() ,当
,当![]() ,
,
则
 ,
,![]() ,
,
其中
![]() .
.
引理3[10] 设![]() 的绝对连续函数,满足
的绝对连续函数,满足
![]()
其中![]() 满足
满足
![]()
则
![]() .
.
定理1的证明
方程(1)分别与![]() 和
和![]() 作
作![]() 内积得到
内积得到
![]() , (12)
, (12)
![]() , (13)
, (13)
(12)+ (13)得到:
![]() , (14)
, (14)
其中![]() .
.
现设(11)的![]() ,令
,令![]() ,则得
,则得
![]() , (15)
, (15)
令(9)的![]() ,则
,则
![]() , (16)
, (16)
结合(15)和(16)得到
![]() , (17)
, (17)
其中![]() .
.
令![]() ,则存在很小的正常数
,则存在很小的正常数![]() ,正常数
,正常数![]() 和
和![]() 使得
使得
![]() , (18)
, (18)
 (19)
(19)
显然,存在![]() 使得
使得
![]() .
.
令![]() ,则(14)
,则(14)
![]() , (20)
, (20)
其中 .
.
由引理2,(20)式可得到
![]() , (21)
, (21)
其中
 ,
,![]() .
.
因此,由(21),
![]() . (22)
. (22)
方程(1)与![]() 作
作![]() 内积得到
内积得到
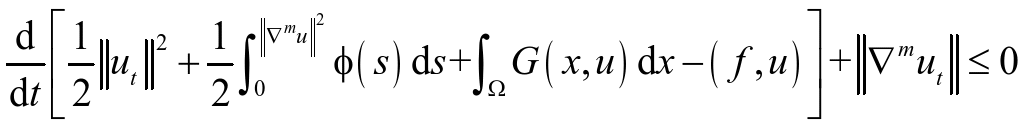 , (23)
, (23)
对(23)在(0,t)上积分,并利用(21),得
![]() . (24)
. (24)
(1)式中的方程分别与![]() ,
,![]() 作
作![]() 内积,得到:
内积,得到:
![]() , (25)
, (25)
 (26)
(26)
由假设![]() 和(22),
和(22),
![]() .
.
所以(25)和(26)化为
![]() , (27)
, (27)
![]() , (28)
, (28)
(27)+ (28)+6(12),得到
 (29)
(29)
其中

由(24)得
![]() ,
,
所以(29)得
 ,
,
由引理3得
![]() . (30)
. (30)
由(2.22)可得定理1的结论.
一.构造近似解
设![]() ,其中
,其中![]() 是
是![]() 在
在![]() 上带有齐次Dirichlet边界的特征值,
上带有齐次Dirichlet边界的特征值,![]() 是对应特征值
是对应特征值![]() 确定的特征函数,根据特征值理论知
确定的特征函数,根据特征值理论知![]() 构成
构成![]() 的标准正交基.固定
的标准正交基.固定![]() ,对于给定的整数
,对于给定的整数![]() ,用
,用![]() 和
和![]() 分别来表示以下空间到其子空间的投影算子:
分别来表示以下空间到其子空间的投影算子:
![]()
根据常微分方程的基本理论,可知在有限时间区间![]() 上存在唯一解
上存在唯一解![]() 满足下列近似方程组:
满足下列近似方程组:
![]() (12)
(12)
其中![]() ,
,![]() ,
,
![]() .
.
满足初始条件![]() ,当
,当![]() 时,在
时,在![]() 中
中![]() .
.
二.先验估计
因需证明在![]() 空间中解的存在性,则式(12)与
空间中解的存在性,则式(12)与![]() 在
在![]() 中作内积,类似于后文式(29),并利用Gronwall不等式,得到
中作内积,类似于后文式(29),并利用Gronwall不等式,得到![]() 空间中解的先验估计:
空间中解的先验估计:
![]() (13)
(13)
由此可知,![]() 在
在![]() 中是一致有界的.
中是一致有界的.
三.极限过程
由式(12)可知
![]()
那么![]() 在空间
在空间![]() 也是一致有界的.
也是一致有界的.
由于![]() 在
在![]() 上有界,所以
上有界,所以![]() 在
在![]() 上有子列强收敛于
上有子列强收敛于![]() ,故存在子列仍用
,故存在子列仍用![]() 来表示,使得
来表示,使得
![]() 在
在![]() 上几乎处处收敛于
上几乎处处收敛于![]() .
.
又因为![]() 是连续函数,所以
是连续函数,所以
![]() 在
在![]() 上几乎处处收敛于
上几乎处处收敛于![]() .
.
另外,利用假设条件![]() ,可得
,可得![]() 在
在![]() 上有界,则
上有界,则
![]() 在
在![]() 上弱*收敛于
上弱*收敛于
![]() .
.
由极限的唯一性得,![]() 在
在![]() 上弱收敛于
上弱收敛于![]() .
.
所以存在子列,仍用![]() 表示,当
表示,当![]() ,使得
,使得
![]() ,在
,在![]() 中弱*收敛;
中弱*收敛;
![]() ,在
,在![]() 中弱*收敛;
中弱*收敛;
![]() ,在
,在![]() 中弱*收敛;
中弱*收敛;
![]() ,在
,在![]() 中弱*收敛;
中弱*收敛;
![]() ,在
,在![]() 中弱收敛;
中弱收敛;
![]() ,在
,在![]() 中弱收敛.
中弱收敛.
当![]() 时,对式(12)取极限,可得
时,对式(12)取极限,可得![]() 是方程(5)(6)(11)的解,满足
是方程(5)(6)(11)的解,满足
![]() .
.
对![]() 设
设![]() 是问题(5)-(6)、(11)关于初值
是问题(5)-(6)、(11)关于初值![]() 的解,再令
的解,再令![]() ,则
,则![]() 和
和![]() 满足
满足
 (14)
(14)
用![]() 与式(14)的第一个方程做
与式(14)的第一个方程做![]() 上的内积,结合假设条件
上的内积,结合假设条件![]() ,则
,则
 (15)
(15)
上述估计用到![]() ,且
,且![]() 是一个合适的正常数.
是一个合适的正常数.
则由式(15),可得
 (16)
(16)
其中 ,再由Gronwall不等式得
,再由Gronwall不等式得
![]() (17)
(17)
式(17)表明在![]() 空间中,
空间中,![]() 连续依赖于初值
连续依赖于初值![]() .则解的唯一性和连续依赖性得证.
.则解的唯一性和连续依赖性得证.
定理2的证明 令![]() ,由(30)式知,
,由(30)式知,![]() 为连续算子半群
为连续算子半群![]() 在
在![]() 中的吸收集,并且对任意的有界集
中的吸收集,并且对任意的有界集![]()
![]() .
.
引理4[11] 设![]() 是完备度量空间
是完备度量空间![]() 上的一个连续半群,则
上的一个连续半群,则![]() 在
在![]() 中存在整体吸引子
中存在整体吸引子![]() 当且仅当
当且仅当
1) ![]() 在
在![]() 中存在有界吸收集;
中存在有界吸收集;
2) ![]() 在
在![]() 上是渐近紧的。
上是渐近紧的。
定理3的证明 令![]() 是问题(1)- (3)式对应于初值
是问题(1)- (3)式对应于初值![]() 的两个解,则
的两个解,则![]() 满足
满足
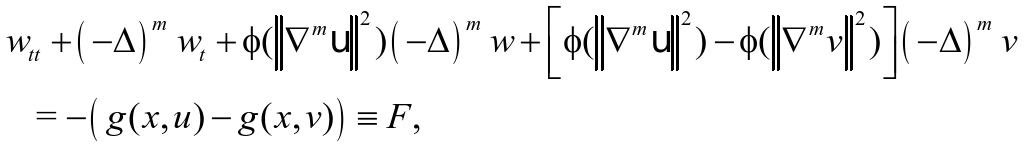 (31)
(31)
![]() (32)
(32)
(31)式分别与![]() 和
和![]() 做
做![]() 内积,利用假设及(30)得到
内积,利用假设及(30)得到
![]() ,
,
 (33)
(33)
 (34)
(34)
 (35)
(35)
(33)![]() +(34) +(35)得到
+(34) +(35)得到
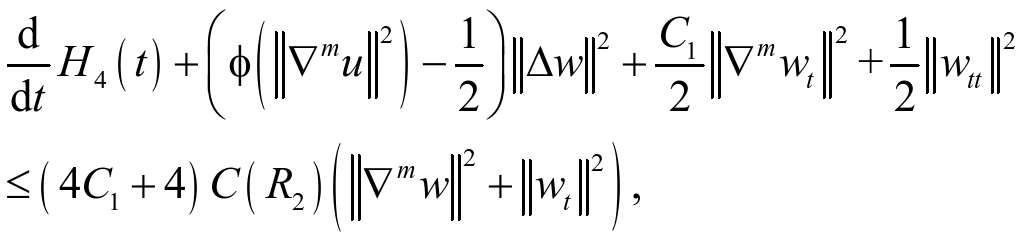 (36)
(36)
其中

记![]() ,则(36)得到
,则(36)得到
![]()
应用Gronwall不等式得到
![]() . (37)
. (37)
设![]() 是
是![]() 中的有界序列,即
中的有界序列,即![]() ,
,![]() 是问题(1)-(3)对应初值
是问题(1)-(3)对应初值![]() 在
在![]() 中的解,下面将证明对任意
中的解,下面将证明对任意![]() 存在一个子序列
存在一个子序列![]() 使得
使得![]() 在
在![]() 中收敛.
中收敛.
事实上对![]() ,取充分大的
,取充分大的![]() 满足
满足![]() ,则
,则![]() 和
和![]() 是原问题在
是原问题在![]() 中的解,则
中的解,则![]() ,且满足
,且满足![]() .
.
由(37)式知

取![]() ,则有
,则有

因为
![]() ,
,
![]() ,
,
即存在子序列,仍记为![]() ,使
,使![]() 在
在![]() 中收敛,即对任意的
中收敛,即对任意的![]() ,存在
,存在![]() 使
使![]() .
.
当![]() 充分大时
充分大时
![]() ,
,
从而有
![]() .
.
即,连续算子半群![]() 是渐近紧的.
是渐近紧的.
由定理2和引理4,定理3得证.
[参考文献]
[1]ZhijianYang.Longtime behavior of the Kirchhoff type equation with strong damping on RN [J].Journal of Differential Equations,2007,242:269-286.
[2] Igor Chueshov.Long-time dynamics of Kirchhoff wave models with strong nonlinear damping [J].Journal of Differential Equations,2012,252:1229-1262.
[3]LV P H,LU J X,LIN G G.Global attractor for a class of nonlinear generalized Kirchhoff models[J].Journal of advances in mathematics,2016,12(8):6452-6462.
[4]Penghui Lv, Xiaojun Lv.Global Attractor for a Class of Nonlinear Generalized Kirchhoff Equation [J].Pure Mathematics,2018,8(6):637-643.
[5]LV P H,LU J X.Inertial Manifolds for a Class of Nonlinear Generalized Kirchhoff Equation [J].
Advances in Applied Mathematics,2018,7(11):1374-1380.
[7]LV P H,LOU R J,LIN G G.Exponential attractors and inertial manifolds for a class of nonlinear generalized Kirchhoff-Boussinesq model[J].Far East Journal of Mathematical Sciences,2017,101(9):1913-1945.
[8]杨志坚,程建玲. Kirchhoff型方程解的渐近行为[J].数学物理学报,2011,31(4):1008-1021.
[9]LV P H,LOU R J,LIN G G.Global attractor for a class of nonlinear generalized Kirchhoff-Boussinesq model[J].International Journal of Modern Nonlinear Theory and Application,2016,5:82-92.
[11]丁鹏燕. 具阻尼Kirchhoff型波动方程的长时间动力学行为[D].郑州:郑州大学数学与统计学院,2017:1-138.
[12]Sun Y T,Gao Y L,LIN G G.The Global Attractors for the Higher-Order Kirchhoff-Type Equation with Nonlinear Strongly Damped Term [J].International Journal of Modern Nonlinear Theory and Application,2016,5:203-217.
[13]Gao Y L, Sun Y T,LIN G G.The Global Attractors and Their Hausdorff and Fractal Dimensions Estimation for the Higher-Order Nonlinear Kirchhoff-Type Equation with Strong Linear Damping [J].International Journal of Modern Nonlinear Theory and Application,2016,5:185-202.
[14]Guoguang Lin, Yunlong Gao.The Global and Exponential Attractors for the Higher-order Kirchhoff-type Equation with Strong Linear Damping [J].Journal of Mathematics Research;,2017,9(4):145-167.