河北建筑工程学院,河北张家口, 075000
摘要:本文通过实测调查的方式采集人体热感觉及其影响因素的数据,根据多元线性回归的方法建立热感觉预测模型,同时采用相对热指标评价乘客热舒适,分别与实际热感觉值对比得出更优模型,并分析误差原因,为相对热指标修正的研究提供新的思路。
关键词:地铁站 多元线性回归 相对热指标
目前截至到2019年12月,我国已建成地铁并投运的城市总计达到42个。地铁以其便利快捷的优势,已经在解决大城市交通问题上做出了重要贡献。由于乘客乘车在地铁站内短暂停留,人体在该环境中热感觉与室内不同。对此,美国运输部提出的相对热指标(RWI)用来评价过渡空间中人体的热舒适性,最终为地铁空调设计温度提供参考[1]。
在2016年,朱培根等人,通过现场测试对南京地铁乘客动态热舒适进行研究,发现采用热感觉投票和相对热指标相结合的方法能更为准确地评价地铁站热环境[2]。近几年,谢浪采集北京地铁数据采用RWI评价了夏季北京地铁的热舒适状况,发现该指标与实际值存在较大偏差[3]。陈思伊计算了西安地铁的RWI发现与实际人体热舒适值存在35%的偏差[4]。但是在相对热指标的优化的研究还比较少,同样也缺乏地铁乘客热感觉预测模型研究。
本文主要通过实际测试和调查的方法获得地铁站热环境参数和人体热感觉结果。考虑影响人体热感觉的多种因素,采用多元回归的方法建立出人体热感觉预测模型。计算相对热指标评价人体热感觉的结果与实际调查结果对比,分析相对热指标评价误差原因,也为预测地铁站乘客热感觉提供新的方法。
在北京地区夏季选择在地铁8号线的南锣鼓巷站和北土城站之间做往返测试。测试前,调查受测人员的基本情况调查表。在实验过程中,受试者每经过一个区域时,调查受测人员的热感觉(冷-3、凉-2、微凉-1、中性 0、微暖 1、暖 2、热 3)情况,并记录人体的活动状态及过渡过程经历的时间,同时测试当前环境的热环境参数。
表一 受试者情况调查表
| 性别 | 人数(N) | 年龄范围(Y) | 身高范围(m) | 体重范围(kg) | 平均服装热阻 (clo) |
| 女性 | 18 | 19-28 | 1.59-1.70 | 47-58 | 0.44 |
| 男性 | 19 | 18-30 | 1.72-1.86 | 56-90 | 0.50 |
人体服装热阻值约为0.5clo,满足夏季人体的舒适需求[5]。受测人员的年龄范围在18岁至30岁之间,男女比例接近1:1。由表二可以看出温度在进站过程中逐渐降低,出站过程温度逐渐升高。相对湿度在30%-50%之间,风速多处于1m/s以内。人体热感觉值整体变化趋势与空气温度的变化趋势相似。乘客进站出站过程的行动速度约为0.9m/s,在站台处等车的时间较长。
表二 人体热感觉情况表
| 所在区域 | 平均温度℃ | 湿度% | 风速m/s | 热感觉平均值 | 活动状态 | 经历时间min |
| 进站口 | 33.3 | 31.5 | 0.7 | 0.68 | 行走0.9m/s | 0.5 |
| 售票处1 | 30.6 | 37.1 | 1.3 | -0.02 | 行走0.9m/s | 1 |
| 站厅1 | 29.5 | 38.8 | 0.6 | -0.19 | 行走0.9m/s | 1.5 |
| 站台1 | 28.0 | 43.7 | 0.5 | -0.23 | 站立等候 | 3 |
| 站台2 | 26.5 | 41.4 | 0.4 | 0.05 | 行走0.9m/s | 1 |
| 站厅2 | 27.7 | 43.5 | 0.6 | 0.02 | 行走0.9m/s | 1.5 |
| 售票处2 | 28.7 | 39.6 | 0.6 | 0.35 | 行走0.9m/s | 1 |
| 出站口 | 29.9 | 36.2 | 0.6 | 1.19 | 行走0.9m/s | 0.5 |
过渡空间连接着两个不同的热环境,RWI是用来反映人员在经过或短暂停留在该区间时的热舒适性的指标。适用于较暖的环境。
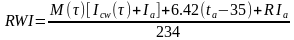 (Pa ≤ 2269Pa) (1)
(Pa ≤ 2269Pa) (1)
 (Pa ≥ 2268Pa) (2)
(Pa ≥ 2268Pa) (2)
式中:M为新陈代谢率,W/m2;τ是过渡过程中经历的时间,s;ta为环境空气的干球温度,℃;Icw为服装热阻,clo;R表示单位皮肤面积的平均辐射得热,W/m2。
当 <360s时
<360s时
 (3)
(3) (4)
(4)
当 ≥360s时
≥360s时
 (5)
(5)
 (6)
(6)
考虑人体运动诱导产生的相对风速Va,计算服装外空气边界层Ia的公式为:
 (7)
(7)
结合RWI的分度与ASHRAE热感觉标度之间的关系确定人体的热感觉值。
表三 相对热指标与ASHRAE热感觉标度的对应关系表
| 热感觉 | 稍凉 | 中性 | 稍暖 | 暖 |
| 热感觉值 | -1 | 0 | 1 | 2 |
| 相对热指标 | 0 | 0.08 | 0.15 | 0.25 |
设自变量y与自变量变量x1,x2,x3,…,xk存在线性关系。第i次测试数据为:(yi ,xi1,xi2 ,xi3,…,xik ),i = 1,2,3,…,n。
y=β0+β1x1+β2x2+···+βkxk (8)
多元线性回归模型可写成如下形式。
 (9)
(9)
公式中,In是n阶单位矩阵;回归方程的回归系数β采用最小二乘估计求得,其公式为:
 (10)
(10)
由于影响人体热舒适的主要因素分为物理因素和生理因素,在过渡空间人体热舒适性研究中需要考虑前一区域热环境和活动状态对当前热舒适性的影响。因此,本文使影响过渡空间人体热舒适的物理因素包括:温度t、相对湿度H、风速Va、两区域的温度差△t、相对湿度差△H和风速差△Va;服装热阻Icw和服装外空气边界层热阻Ia;生理因素包括:性别、年龄、身高、体重和新陈代谢率M(τ)。
在多元回归模型中,将性别用数值代替,其中男性用1表示,女性用0表示,将人体的身高、体重用能表示人体肥胖程度的身体指数值代替(BMI=体重比身高的平方,Kg/(m)2),确定为多元线性回归模型中的自变量为12项。进行显著性检验,取显著性水平为0.05,剔除与热舒适性不显著的自变量,并结合最小二乘估计出的回归系数,可确定多元回归方程。
根据多元回归理论拟合出人体热感觉计算公式如下。
Y = -5.135+0.186ta+0.074△ta+0.9△H+0.043Y-0.012M(τ)
公式中与人体热感觉相关的参数分别为环境温度、与前一区域的温差和相对湿度差、年龄和活动状态。分别根据以上公式和相对热指标计算热感觉值并与实际值对比得到图一。人体在进站过程中,热感觉值逐渐变低,出站过程则相反。RWI评价热感觉的结果与实际值存在偏差,但整体变化趋势与实际情况相似。而采用多元回归拟合公式计算的结果与实际值比较接近,整体变化趋势也与实际变化的相似度较高。

图一 各区域热感觉图
通过计算预测值与实际热感觉值的均方误差,观察RWI和多元线性回归公式预测结果的准确度,得到图二。图二中根据多元线性回归公式计算得热感觉值与实际值的均方误差较接近小,说明预测结果比较准确,而RWI评价结果的准确度不高。相对热指标的计算过程虽然考虑了动态过程中人体的新陈代谢率和服装热阻变化,但是从多元线性回归公式中可以看出,乘客的热感觉值与两区域的温差和湿度差也存在显著性关系。

图二 各区域预测结果的均方误差图
根据多元线性回归理论分析人体热感觉与其影响因素数据之间的关系,建立的地铁乘客热感觉预测模型,比RWI更能准确度的评价地铁站人体热感觉情况。两空间的空气温度差和相对湿度差与热感觉存在显著性关系,对以后相对热指标的修正研究提供参考。
[1]Subway Environmental Design Handbook (Volume 1), United States Department of Transportation, 1976
[2]朱培根,王春旺,仝晓娜,宋桦,李晓昀.地铁站乘客动态热舒适评价研究[J].暖通空调,2016,46(02):101-104+40.
[3]谢浪,基于实测调查和相对热指标的北京地铁车站热舒适研究[D].北京工业大学,2017.
[4]陈思伊. 西安地铁车站热环境评价及设计温度研究[D].长安大学,2018.
[5]朱颖心,《建筑环境学》第三版2010.10,P97