成都市晋阳小学 四川 成都 610057
内容摘要:
根据六年级总复习教材内容设置,结合学生实际情况,革新教学内容,将分数、百分数乘除法解决问题融合在一起进行复习整理,复习整理过程中,抓乘法意义的这根知识线,让学生经历整理知识的过程,理清涉及的知识点、弄清知识之间的联系,形成完整的数学认知结构,提升学生思维品质。
关键词 :知识点、知识线
六下是小学阶段的最后一个学期,在完成小学数学全部内容的学习之后,教材设置了四个领域的总复习。现以六年级下册分数、百分数乘除法解决问题的整理与复习课例进行简述。分数乘法和整数乘法意义相同,都是求几个相同加数和的简便运算;分数除法是分数乘法的逆运算;分数表示分率时和百分数可以互换。
课前,借知识线索明确任务,提高梳理质量。
整理的过程虽看似繁琐,但让学生完整地经历至关重要。课前的梳理需要明确整理的任务,有了任务的驱使,才会促使学生主动参与整理的过程。有核心问题的整理任务会提升学生的梳理质量。下表是六年级两个班级课前自主梳理知识的情况:
| 班级 | 六年级七班(38人) | 六年级二班(43人) |
| 整理 内容 | 北师大版五下分数乘法(P22-35)、分数除法(P55-64)、百分数的应用(P87-99) | 北师大版五下分数乘法(P22-35)、分数除法(P55-64)、六上分数混合运算(P21-31)、百分数(P39-56) |
| 课前整理要求 | 1.整理五下、六上分数、百分数乘除法应用题; 2.同类型选1道例题; | 18道例题只列式不计算。 2.整理分数、百分数乘除法应用题例题。 ①将18道例题按一定的标准分类整理; ②思考每一类题之间有什么联系?不同类题之间有什么区别? |
| 学生整理结果 | ①列举部分例题(11人) ②整理知识点(9人) ③按课题顺序分六类(2人) ④按分数、百分数分两类(7人); ⑤按分数乘法1步、2步、分数除法1步、2步分四类(2人); ⑥分数乘、除法、百分数(4人) ⑦按分数乘、除、百分数乘、除法分四类(2人) | ①列举部分例题(8人) ②按册数分类整理(1人) ③按分数、百分数分两类(11人) ④按等量关系分为三类(21人) ⑤按三个等量关系+利息,分为四类(1人) |
11人采取简单罗列部分例题的方式整理;9人属于知识点的罗列;17人根据分类标准整理:2人按课题顺序整理,13人按分数和百分数分类整理,2人按解题步骤整理。学生的经历浮于面上,没有触及例题中量与量之间的关系,整个班级的整理质量不高。
学生在解答18道例题的过程中,有了列式要求,必定会分析题中量与量的关系、例题的解题思路和方法。分类时既要考虑分类的标准,有了这些明确的要求,学生整理笔记的质量有了明显提高。虽然学生整理层次不同,但他们都能围绕分类梳理所学知识进行分类。
二、课中,围绕知识线索交流碰撞,引发深度学习
著名数学家陈省身先生指出:“数学是自己思考的产物。首先要能够思考起来,用自己的见解和别人的见解交换,会有很好的效果。”当学生独立建构知识的体系后,应营造和谐宽松的安全氛围,适时干预,引发学生的深度对话与思考。
1.小组思维碰撞,初次审视整理笔记
每个学生整理的笔记,都是自身思维外显的成果,将整理的思维过程用文字呈现出来后,还应积极地用语言表达出来。课堂的开始,采取4人小组交流讨论的方式,提供足够的空间与时间,给予每个学生表达思维过程的机会。
2.全班思维交锋,寻求整理笔记的最优化
首先分享的是按课题顺序整理的学生,从他的分享中,学生回顾了学习分数、百分数乘除法的顺序,明确这是我们梳理知识很重要的第一步。
【教学片段】
生1:我先按分数、百分数分为两类,然后分数中我又继续往下分,分成求单位“1”、求比较量、求分率三类,百分数我按求单位“1”、求比较量、求百分率分成三类。
生2:我觉得你的分类很具体,但是你的分数和百分数继续分下去是差不多的。
师:哪里差不多?
生2:他分类时分数按求单位“1”、求比较量、求分率分为三类,百分数也是呀!
生4:例如第1题,没有改变题意,也没改变解题思路,计算结果都等于3,所以我觉得它们的性质是一样,这样分类整理价值不大。
有了这里水到渠成的交流讨论,学生一致认为可以按3个等量关系进行分类整理。此时,按量与量关系分为三类的学生进行了具体的分享展示。
3.教师适时干预,引发讨论走向数学本质
教师抛出问题,继续追问:6× ,12×
,12×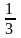 ×
× ,40×(1-
,40×(1-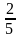 )对应的三道例题,解题步骤不一样,为什么分为一类?学生在讨论中得出,虽然三道例题解决的步骤不一样,但它们都是知道单位“1”和分率,只不过第1题单位“1”、分率直接已知,一步可以解决。第2题需两步解决。第3题需要先解决对应的分率,需要两步解决。归根结底它们都是求一个数的几分之几是多少,只是有的量没有直接告诉而已。
)对应的三道例题,解题步骤不一样,为什么分为一类?学生在讨论中得出,虽然三道例题解决的步骤不一样,但它们都是知道单位“1”和分率,只不过第1题单位“1”、分率直接已知,一步可以解决。第2题需两步解决。第3题需要先解决对应的分率,需要两步解决。归根结底它们都是求一个数的几分之几是多少,只是有的量没有直接告诉而已。
看似杂乱无章的18道例题,由相同等量关系串成了知识线,由不同的未知量分成了三类。根据纵的观察,学生发现了同类等量关系的联系。根据横的比较,学生提出这三类题,归根结底就是一类题。在“生生”的深度对话中,学生对数学知识的理解及知识结构的梳理,让原来认识上有所欠缺的学生能完善认知结构,找到知识间的内在联系。
三、课后,借知识线完善整理迁移应用,拓展思维发展。
布鲁纳说: “一门课程在它的教学进展中,应反复地回到这些基本观念,以这些基本观念为基础,直至学生掌握了与这些观念相适应的完全形式的体系为止。”学生学习的过程中,梳理自己所学的知识,完善自己的整理笔记,整理出有特色有深度的复习笔记,逐步积累整理复习的活动经验,养成课后复习的良好习惯。
参考文献
[1]刘贤虎 论小学数学复习课的“梳理”和“练习” 厦门广播电视大学学报 2018年4月 第2期
[2]朱德江 这才是“深度学习”-基本特征、教学策略和课堂样态 上海悦远教育 2018年10月